题目内容
已知un=an+an-1b+an-2bn+…+abn-1+bn(n∈N*,a＞0,b＞0).(1)当a=b时,求数列{un}的前n项和Sn;
(2)求
.
解:(1)当a=b时,un=(n+1)an.这时数列{un}的前n项和
Sn=2a+3a2+4a3+…+nan-1+(n+1)an. ①
①式两边同乘以a,得
aSn=2a2+3a3+4a4+…+nan+(n+1)an+1. ②
①式减去②式,得
(1-a)Sn=2a+a2+a3+…+an-(n+1)an+1.
若a≠1,
(1-a)Sn=-(n+1)an+1+a.
Sn=+
=
.
若a=1,
Sn=2+3+…+n+(n+1)=
.
(2)由(1),当a=b时,un=(n+1)an,则
=
=
=a.
当a≠b时,
un=an+an-1b+…+abn-1+bn
=an［1+
+(
)2+…+(
)n］
=an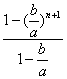
=
(an+1-bn+1).
此时,
=
.
若a＞b＞0,
=
=
=a.
若b＞a＞0,
=
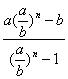=b.
练习册系列答案
相关题目
．
．
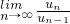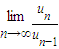