题目内容
【题目】已知函数![]() .
.
⑴从区间![]() 内任取一个实数
内任取一个实数![]() ,设事件
,设事件![]() 表示“函数
表示“函数![]() 在区间
在区间![]() 上有两个不同的零点”,求事件
上有两个不同的零点”,求事件![]() 发生的概率;
发生的概率;
⑵若联系掷两次一颗均匀的骰子(骰子六个面上标注的点数分别为![]() )得到的点数分别为
)得到的点数分别为![]() 和
和![]() ,记事件
,记事件![]() 表示“
表示“![]() 在
在![]() 上恒成立”,求事件
上恒成立”,求事件![]() 发生的概率.
发生的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)利用题意考查![]() ,据此得到关于实数
,据此得到关于实数![]() 的不等式组即可求得实数
的不等式组即可求得实数![]() 的取值范围,然后求解事件
的取值范围,然后求解事件![]() 发生的概率.
发生的概率.
(2)结合题意分别讨论![]() ;
; ![]() ;
; ![]() ;
; ![]() ,然后利用分类加法计数原理求解满足题意的基本事件个数,然后结合古典概型的计算公式计算事件
,然后利用分类加法计数原理求解满足题意的基本事件个数,然后结合古典概型的计算公式计算事件![]() 发生的概率.
发生的概率.
试题解析:
(1)因为函数![]() 在区间
在区间![]() 上有两个不同的零点,
上有两个不同的零点,
所以![]() ,即
,即![]() 有两个不同的正根
有两个不同的正根![]() 和
和![]() ,
,
所以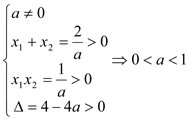 ,所以
,所以![]() .
.
(2)由已知![]() ,所以
,所以![]() 即
即![]() 在
在![]() 上恒成立,
上恒成立,
故需且只需![]() (*).
(*).
当![]() 时,
时,![]() 适合(*);当
适合(*);当![]() 时,
时,![]() 适合(*);当
适合(*);当![]() 时,
时,![]() 均 适合(*);
均 适合(*);
当![]() 时,
时,![]() 适合(*).满足(*)的基本事件个数为
适合(*).满足(*)的基本事件个数为 ![]() .而基本事件总数为
.而基本事件总数为![]() ,
,
所以![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目