题目内容
定理:若函数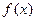 在闭区间[m,n]上是连续的单调函数,且
在闭区间[m,n]上是连续的单调函数,且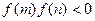 ,则存在唯一一个
,则存在唯一一个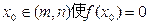 。已知
。已知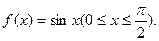
(1)若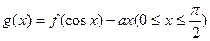 是减函数,求a的取值范围。
是减函数,求a的取值范围。
(2)是否存在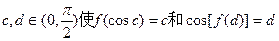 同时成立,若存在,指出c、d之间的等式关系,若不存在,请说明理由。
同时成立,若存在,指出c、d之间的等式关系,若不存在,请说明理由。
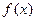 在闭区间[m,n]上是连续的单调函数,且
在闭区间[m,n]上是连续的单调函数,且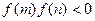 ,则存在唯一一个
,则存在唯一一个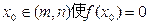 。已知
。已知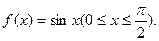
(1)若
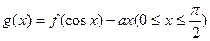 是减函数,求a的取值范围。
是减函数,求a的取值范围。(2)是否存在
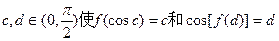 同时成立,若存在,指出c、d之间的等式关系,若不存在,请说明理由。
同时成立,若存在,指出c、d之间的等式关系,若不存在,请说明理由。(1)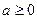
(2)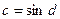
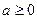
(2)
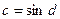
(1)
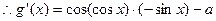
依题意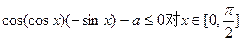 恒成立
恒成立
即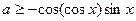
显然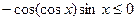
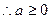 ,故a的取值范围是
,故a的取值范围是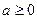 …………6分
…………6分
(2)由(1)知:当a=1时,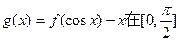 上是减函数
上是减函数
且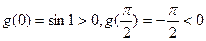
∴存在唯一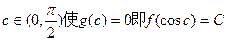 …………8分
…………8分
同理由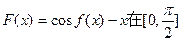 上是减函数
上是减函数
且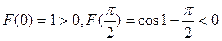
知存在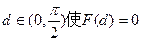
即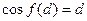 成立 …………10分
成立 …………10分
由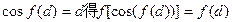
及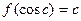 的唯一性知
的唯一性知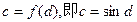
综上可知,存在c,d使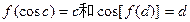 同时成立,
同时成立,
且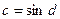 …………13分
…………13分

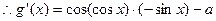
依题意
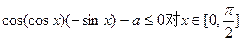 恒成立
恒成立即
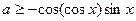
显然
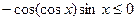
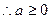 ,故a的取值范围是
,故a的取值范围是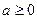 …………6分
…………6分(2)由(1)知:当a=1时,
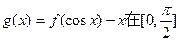 上是减函数
上是减函数且
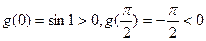
∴存在唯一
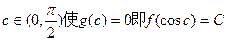 …………8分
…………8分同理由
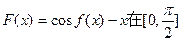 上是减函数
上是减函数且
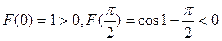
知存在
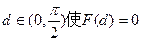
即
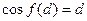 成立 …………10分
成立 …………10分由
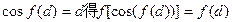
及
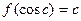 的唯一性知
的唯一性知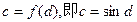
综上可知,存在c,d使
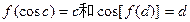 同时成立,
同时成立,且
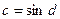 …………13分
…………13分
练习册系列答案
相关题目
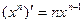 ,
,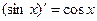 ,
,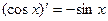 ,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。
,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。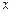 (
(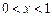 ),则出厂价相应提高的比例为
),则出厂价相应提高的比例为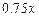 ,同时预计年销售量增加的比例为
,同时预计年销售量增加的比例为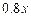 。已知年利润
。已知年利润 (出厂价
(出厂价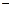 投入成本)
投入成本)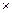 年销售量。
年销售量。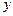 与投入成本增加的比例
与投入成本增加的比例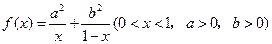 的最值。
的最值。 为曲线
为曲线 在点(1,0)处的切线,直线
在点(1,0)处的切线,直线 为该曲线的另一条切线,且
为该曲线的另一条切线,且

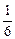 处的切线的倾斜角是
处的切线的倾斜角是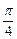
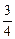 π
π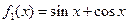 ,记
,记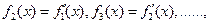
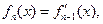
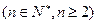 ,则
,则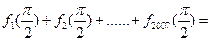 ________.
________.