题目内容
 已知圆G过点A(2,0),B(5,3),C(3,-1),过点A的直线l1,l2,分别交圆G于点M,N(M,N不与A重合),且它们的斜率k1,k2满足k1+k2=0.
已知圆G过点A(2,0),B(5,3),C(3,-1),过点A的直线l1,l2,分别交圆G于点M,N(M,N不与A重合),且它们的斜率k1,k2满足k1+k2=0.(Ⅰ)求圆G的方程;
(Ⅱ)求证:直线MN的斜率为定值.
分析:(Ⅰ)设圆G的方程为x2+y2+Dx+Ey+F=0,把圆经过的三个点的坐标代入求得待定系数,从而得到圆G的方程.
(Ⅱ)设直线l1的方程为y=k1(x-2),代入圆的方程可求得M的坐标,同理可求的N的坐标,利用斜率公式化简MN的
斜率得到定值.
(Ⅱ)设直线l1的方程为y=k1(x-2),代入圆的方程可求得M的坐标,同理可求的N的坐标,利用斜率公式化简MN的
斜率得到定值.
解答:解:(Ⅰ)设圆G的方程为x2+y2+Dx+Ey+F=0,因为圆G过点A(2,0),B(5,3),C(3,-1),
所以,
,解得
,所以圆G的方程为x2+y2-8x-2y+12=0.
(Ⅱ)设直线l1的方程为y=k1(x-2),
由
消去y 得 (k12+1)x2-2(2k12+k1+4)x+(4k12+4k1+12)=0,
解得
或
,所以M(
,
).
同理N(
,
),又k1+k2=0,所以N(
,
),
kMN=
=2(定值),故结论成立.
所以,
|
|
(Ⅱ)设直线l1的方程为y=k1(x-2),
由
|
解得
|
|
2
| ||
|
2
| ||
|
同理N(
2
| ||
|
2
| ||
|
2
| ||
|
2
| ||
|
kMN=
| ||||
|
点评:本题考查用待定系数法求圆的一般式方程,直线和圆相交的性质,求出M、N两点的坐标是解题的难点.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
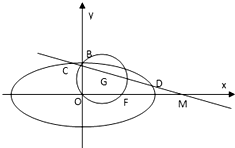 如图,已知圆G:x2+y2-2x-
如图,已知圆G:x2+y2-2x-