题目内容
关于x的方程(1-a)x2+2ax+2-3a=0至少有一个正根,则a∈________.
( ,2]
,2]
分析:①当二次项的系数 1-a=0时,经检验满足条件.②当二次项的系数 1-a≠0时,则有△≥0,分两个根一个为正数另一个是非负数,和两个根一正、一负根两种情况,
分别求得a的取值范围.综合①②,把得到的a的取值范围再取并集,即得所求.
解答:①当二次项的系数 1-a=0时,即a=1时,方程即 2x-1=0,解得x= ,故满足条件.
,故满足条件.
②当二次项的系数 1-a≠0时,即a≠1时,由判别式△=4a2-4(1-a)(2-3a)=-4(a-2)(2a-1)≥0,解得 ≤a≤2.
≤a≤2.
若两个根一个为正数另一个是非负数,则两根之和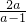 >0 且两根之积
>0 且两根之积 ≥0,解得a<0,或a≥1.
≥0,解得a<0,或a≥1.
综合可得,1≤a≤2.
若方程有一正、一负根,则两根之积 <0,解得
<0,解得  <a<1.
<a<1.
综合可得, <a<1.
<a<1.
综合①②可得,a的取值范围为( ,2],
,2],
故答案为 ( ,2].
,2].
点评:本题考查一元二次方程的根的分布与系数的关系,考查分类讨论思想,转化思想,是中档题.
 ,2]
,2]分析:①当二次项的系数 1-a=0时,经检验满足条件.②当二次项的系数 1-a≠0时,则有△≥0,分两个根一个为正数另一个是非负数,和两个根一正、一负根两种情况,
分别求得a的取值范围.综合①②,把得到的a的取值范围再取并集,即得所求.
解答:①当二次项的系数 1-a=0时,即a=1时,方程即 2x-1=0,解得x=
 ,故满足条件.
,故满足条件.②当二次项的系数 1-a≠0时,即a≠1时,由判别式△=4a2-4(1-a)(2-3a)=-4(a-2)(2a-1)≥0,解得
 ≤a≤2.
≤a≤2.若两个根一个为正数另一个是非负数,则两根之和
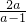 >0 且两根之积
>0 且两根之积 ≥0,解得a<0,或a≥1.
≥0,解得a<0,或a≥1.综合可得,1≤a≤2.
若方程有一正、一负根,则两根之积
 <0,解得
<0,解得  <a<1.
<a<1.综合可得,
 <a<1.
<a<1.综合①②可得,a的取值范围为(
 ,2],
,2],故答案为 (
 ,2].
,2].点评:本题考查一元二次方程的根的分布与系数的关系,考查分类讨论思想,转化思想,是中档题.

练习册系列答案
相关题目