题目内容
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA=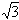 ,,AA1=
,,AA1=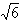 ,M为侧棱CC1上一点,AM⊥BA1。
,M为侧棱CC1上一点,AM⊥BA1。
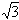 ,,AA1=
,,AA1=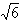 ,M为侧棱CC1上一点,AM⊥BA1。
,M为侧棱CC1上一点,AM⊥BA1。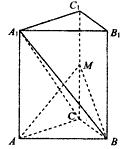
(1)求证:AM⊥平面A1BC;
(2)求二面角B-AM-C的大小;
(3)求点C到平面ABM的距离。
(2)求二面角B-AM-C的大小;
(3)求点C到平面ABM的距离。
解:(1)在直三棱柱ABC-A1B1C1中,易知面ACC1A1⊥面ABC,
∵∠ACB = 90°,
∴BC⊥面ACC1A1,
∵AM 面ACC1A1
面ACC1A1
∴BC⊥AM
∵AM⊥BA1,且BC∩BA1=B
∴AM⊥平面A1BC;
(2)以C为原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则
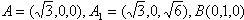
设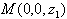
∵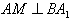
∴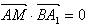
即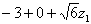 =0
=0
故
所以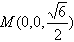
设向量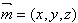 为平面AMB的法向量,则
为平面AMB的法向量,则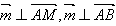
则 即
即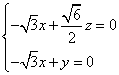
令x=1的平面AMB的一个法向量为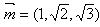
显然向量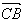 是平面AMC的一个法向量
是平面AMC的一个法向量

易知,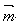 与
与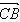 所夹的角等于二面角B - AM - C的大小,
所夹的角等于二面角B - AM - C的大小,
故所求二面角的大小为45°。
(3)向量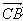 在法向量
在法向量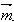 上的投影的长
上的投影的长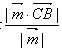 即为所求距离
即为所求距离
∴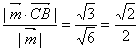
∴点C到平面ABM的距离为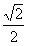 。
。
∵∠ACB = 90°,
∴BC⊥面ACC1A1,
∵AM
 面ACC1A1
面ACC1A1 ∴BC⊥AM
∵AM⊥BA1,且BC∩BA1=B
∴AM⊥平面A1BC;
(2)以C为原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则
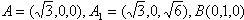
设
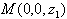
∵
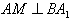
∴
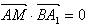
即
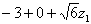 =0
=0故

所以
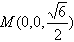
设向量
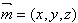 为平面AMB的法向量,则
为平面AMB的法向量,则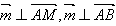
则
 即
即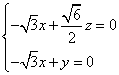
令x=1的平面AMB的一个法向量为
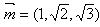
显然向量
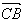 是平面AMC的一个法向量
是平面AMC的一个法向量 
易知,
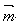 与
与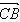 所夹的角等于二面角B - AM - C的大小,
所夹的角等于二面角B - AM - C的大小,故所求二面角的大小为45°。
(3)向量
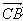 在法向量
在法向量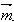 上的投影的长
上的投影的长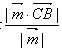 即为所求距离
即为所求距离∴
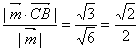
∴点C到平面ABM的距离为
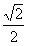 。
。
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目




