题目内容
【题目】设函数f(x)=cos(ωx+φ)(ω>0,﹣ ![]() <φ<0)的最小正周期为π,且f(
<φ<0)的最小正周期为π,且f( ![]() )=
)= ![]() .
. 
(1)求ω和φ的值;
(2)在给定坐标系中作出函数f(x)在[0,π]上的图象.
【答案】
(1)解:周期T= ![]() =π,∴ω=2,
=π,∴ω=2,
∵f( ![]() )=cos(
)=cos( ![]() φ)=cos(
φ)=cos( ![]() +φ)=﹣sinφ=
+φ)=﹣sinφ= ![]() .
.
∵﹣ ![]() <φ<0∴φ=﹣
<φ<0∴φ=﹣ ![]()
(2)解:由(1)知f(x)=cos(2x﹣ ![]() ),列表如下:
),列表如下:
2x﹣ | ﹣ | 0 |
| π |
|
|
x | 0 |
|
|
|
| π |
f(x) |
| 1 | 0 | ﹣1 | 0 |
|
在给定坐标系中作出函数f(x)在[0,π]上的图象如下:
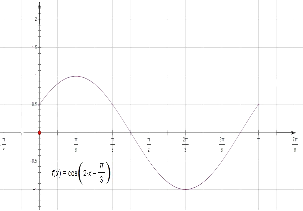
【解析】(1)由周期公式T= ![]() =π,可得ω=2,由f(
=π,可得ω=2,由f( ![]() )=cos(
)=cos( ![]() φ)=cos(
φ)=cos( ![]() +φ)=﹣sinφ=
+φ)=﹣sinφ= ![]() 及﹣
及﹣ ![]() <φ<0可得φ=﹣
<φ<0可得φ=﹣ ![]() .(2)列表,描点即用五点法作出函数y=cos(2x﹣
.(2)列表,描点即用五点法作出函数y=cos(2x﹣ ![]() )的图象.
)的图象.
【考点精析】关于本题考查的五点法作函数y=Asin(ωx+φ)的图象,需要了解描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线)才能得出正确答案.

【题目】学校组织学生参加某项比赛,参赛选手必须有很好的语言表达能力和文字组织能力.学校对10位已入围的学生进行语言表达能力和文字组织能力的测试,测试成绩分为![]() 三个等级,其统计结果如下表:
三个等级,其统计结果如下表:
文字组织能力 |
|
|
|
| 2 | 2 | 0 |
| 1 |
| 1 |
| 0 | 1 |
|
由于部分数据丢失,只知道从这10位参加测试的学生中随机抽取一位,抽到语言表达能力或文字组织能力为![]() 的学生的概率为
的学生的概率为![]() .
.
(Ⅰ)求![]() ,
, ![]() 的值;
的值;
(Ⅱ)从测试成绩均为![]() 或
或 ![]() 的学生中任意抽取2位,求其中至少有一位语言表达能力或文字组织能力为
的学生中任意抽取2位,求其中至少有一位语言表达能力或文字组织能力为![]() 的学生的概率.
的学生的概率.
【题目】某批次的某种灯泡![]() 个,对其寿命进行追踪调查,将结果列成频率分布表如下,根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个,对其寿命进行追踪调查,将结果列成频率分布表如下,根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于![]() 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于![]() 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
寿命 (天) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(1)根据频率分布表中的数据,写出![]() 的值;
的值;
(2)某人从这![]() 个灯泡中随机地购买了
个灯泡中随机地购买了![]() 个,求此灯泡恰好不是次品的概率;
个,求此灯泡恰好不是次品的概率;
(3)某人从这批灯泡中随机地购买了![]() 个,如果这
个,如果这![]() 个灯泡的等级情況恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情況恰好与按三个等级分层抽样所得的结果相同,求![]() 的最小值.
的最小值.