Question

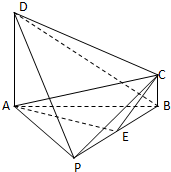在四棱锥P-ABCD，PA=PB=AD=AB=4BC=4，E为PB的中点，AD∥BC，且AD⊥面PAB
（1）求证：BD⊥CE
（2）求二面角E-AC-B的余弦值大小．

Answer 1

分析：（1）在四棱锥P-ABCD中，取DP的中点F，则EF是三角形PBD的中位线，故有BD∥EF ①．再利用勾股定理证明EF⊥CE ②，可得BD⊥CE．
（2）由题意可得平面ABCD⊥平面PAB，过点E作EG⊥AB，G为垂足；再过点G作GH⊥AC，H为垂足，可证∠EHG为二面角E-AC-B的平面角．利用等面积法求得 EG和EH的值．再求得sin∠EHG=

EG

EH

的值，可得cos∠EHG 的值，即为所求．

解答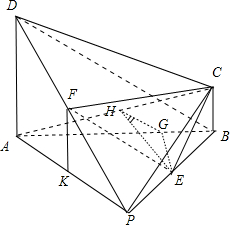：解：（1）在四棱锥P-ABCD中，由于E为PB的中点，
再取DP的中点F，AP的中点为K，
则FK是三角形PAD的中位线，FK平行且等于

1

2

AD；
EF是三角形PBD的中位线，故有BD∥EF ①．
再根据PA=PB=AD=AB=4BC=4，AD∥BC，且AD⊥面PAB，
可得EF=

1

2

BD=2

2

，CE=

BE2+BC2

=

5

，
FC=

BK2+(FK-BC)2

=

(2 3 )2+1

=

13

．
显然有 CE²+EF²=FC²，∴EF⊥CE ②．
由①、②可得BD⊥CE．
（2）由题意可得平面ABCD⊥平面PAB，过点E作EG⊥AB，G为垂足，则EG⊥平面ABCD．
再过点G作GH⊥AC，H为垂足，则有三垂线定理可得，EH⊥AC，∴∠EHG为二面角E-AC-B的平面角．
由

1

2

•AE•BE=

1

2

AB•EG，可得

1

2

×2

3

×2=

1

2

×4×EG，解得  EG=

3

．
由于AD⊥面PAB，AD∥BC，∴BC⊥面PAB，∴CPB⊥面PAB．
再根据等边三角形种AE⊥PB，∴AE⊥平面PBC，∴AE⊥EC．
再根据

1

2

•AE•EC=

1

2

•AC•EH，可得

1

2

×2

3

×

5

=

1

2

×

17

×EH，解得 EH=2

15 17

．
直角三角形EGH中，sin∠EHG=

EG

EH

=

3

2 15 17

，
∴cos∠EHG=

9 60

=

15

10

，即二面角E-AC-B的余弦值为

15

10

．

点评：本题主要考查直线和平面垂直的判定与性质，用等面积法求三角形某边上的高线长，求二面角的平面角，体现了转化的数学思想，属于中档题．