题目内容
给定两个长度均为 的平面向量
的平面向量 和
和 ,它们的夹角为
,它们的夹角为 ,点
,点 在以为
在以为 圆心的
圆心的 圆弧上运动,如图所示,若
圆弧上运动,如图所示,若
 +
+ ,其中
,其中 ,
,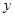
 ,则
,则 的最大值是 ( )
的最大值是 ( )
A. | B. | C. | D. |
D
解析试题分析:如下图建立平面直角坐标系,∵ ,∴
,∴ ,
,
又∵
 +
+ ,∴
,∴ ,又∵C在圆上,
,又∵C在圆上,
∴ ,化简得:
,化简得: ,令
,令 ,代入方程,可得
,代入方程,可得 ,∴
,∴ ,∴
,∴ 的最大值为
的最大值为 .
.
考点:平面向量的线性运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知正六边形 ,在下列表达式①
,在下列表达式① ;②
;② ;
;
③ ;④
;④ 中,等价的有
中,等价的有
A. 个 个 | B. 个 个 | C. 个 个 | D. 个 个 |
在 ABCD中,错误的式子是( )
ABCD中,错误的式子是( )
A. | B. |
C. | D. |
设 都是非零向量,下列四个条件中,一定能使
都是非零向量,下列四个条件中,一定能使 成立的是( )
成立的是( )
A. | B. | C. | D. |
已知向量 =(x,1),
=(x,1), =(4,x),若向量
=(4,x),若向量 和
和 方向相同,则实数x的值是( )
方向相同,则实数x的值是( )
| A.﹣2 | B.2 | C.0 | D. |
在△ABC中,M为边BC上任意一点,N为AM中点, ,则λ+μ的值为( )
,则λ+μ的值为( )
A. |
B. |
C. |
| D.1 |
 ,则向量
,则向量 ( )
( )



 的内角A、B、C的对边长分别为a、b、c,且3
的内角A、B、C的对边长分别为a、b、c,且3 +3
+3 -3
-3 =4
=4 bc .
bc . 的值.
的值.