题目内容
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
(Ⅰ)证明:PQ∥平面ACD;
(Ⅱ)求AD与平面ABE所成角的正弦值.
(Ⅰ)证明:PQ∥平面ACD;
(Ⅱ)求AD与平面ABE所成角的正弦值.

| (Ⅰ)证明:因为P,Q分别为AE,AB的中点, 所以PQ∥EB, 又DC∥EB, 因此PQ∥DC, 从而PQ∥平面ACD. |
|
|
(Ⅱ)解:如图,连结CQ,DP, |
 |

练习册系列答案
相关题目
 ,
, 。
。 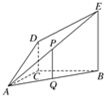 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.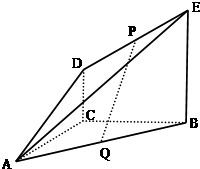 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=90°,P、Q分别为DE、AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=90°,P、Q分别为DE、AB的中点.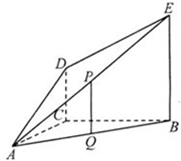 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.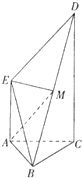 如图,DC⊥平面ABC,EA∥DC,AB=AC=AE=
如图,DC⊥平面ABC,EA∥DC,AB=AC=AE=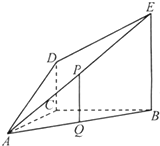 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.