题目内容
（本题满分14分）在数列
中，已知
.
(1)证明数列
是等比数列；(2) 
为数列
的前
项和，求
的表达式；
（3）在（2）的条件下，若存在自然数
使
对
恒成立，求
的最小值.
(Ⅰ) 略 (Ⅱ) 
（Ⅲ）
解析:
（1）解: ∵ 
, ∴
,
∴ 
, 又
,
∴ 数列
是以2为公比、以-2为首项的等比数列。
(2)由(1)得: 
， ∴ 
，
,
∴
,
令
, 则
,
两式相减得: 
∴ 
, 即。
（3）
练习册系列答案
相关题目
（
），
，动点
的轨迹为T．
时，已知
、
，试探究是否存在这样的点
： 
？若存在，求出点Q的坐标，若不存在，说明理由．
中，已知圆
，
．
的直线
被圆
截得的弦长为
，求直线
是以1为半径，圆心在圆
：
上移动的动圆 ，若圆
分别作圆
的两条切线
，切点为
，求
的取值范围 ；
同时平分圆
的周长、圆
中，角
、
、
所对应的边分别为
、
、
，且满足
，求实数
的值。
，求
的值.
的正方体
中,
是线段
的中点,底面ABCD的中心是F.
^
； 
；
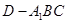的体积。
的左、右焦点分别为F1、F2．F2也是抛物线C2：
的焦点，点M为C1与C2在第一象限的交点，且
．
，直线l∥MN，且与C1交于A、B两点，若
·
=0，求直线l的方程．