题目内容
直线y=x+1与椭圆m x 2+n y 2=1( m,n>0 )相交于A,B两点,弦AB的中点的横坐标是- ,则双曲线
,则双曲线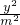 -
- =1的两条渐近线所夹的锐角等于
=1的两条渐近线所夹的锐角等于
- A.2arctan2
- B.2arctan

- C.π-2arctan2
- D.π-2arctan

B
分析:把直线与椭圆方程联立消去y,根据韦达定理求得x1+x2的表达式,进而根据x1+x2=- ,求得n和m的关系,求得渐近线的斜率,进而根据两条渐近线夹角为渐近线的倾斜角的两倍,进而求得答案.
,求得n和m的关系,求得渐近线的斜率,进而根据两条渐近线夹角为渐近线的倾斜角的两倍,进而求得答案.
解答:把直线与椭圆方程联立 消去y得(m+n)x2+2nx+n-1=0
消去y得(m+n)x2+2nx+n-1=0
∴x1+x2=- =-
=-
∴ =
=
则双曲线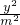 -
- =1的一条渐近线y=
=1的一条渐近线y= x的倾斜角为arctan
x的倾斜角为arctan ;
;
∴两条渐近线所夹的锐角等于2arctan
故选B.
点评:本小题主要考查双曲线的简单性质、两直线的夹角、直线与圆锥曲线的综合问题等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.
分析:把直线与椭圆方程联立消去y,根据韦达定理求得x1+x2的表达式,进而根据x1+x2=-
 ,求得n和m的关系,求得渐近线的斜率,进而根据两条渐近线夹角为渐近线的倾斜角的两倍,进而求得答案.
,求得n和m的关系,求得渐近线的斜率,进而根据两条渐近线夹角为渐近线的倾斜角的两倍,进而求得答案.解答:把直线与椭圆方程联立
 消去y得(m+n)x2+2nx+n-1=0
消去y得(m+n)x2+2nx+n-1=0∴x1+x2=-
 =-
=-
∴
 =
=
则双曲线
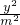 -
- =1的一条渐近线y=
=1的一条渐近线y= x的倾斜角为arctan
x的倾斜角为arctan ;
;∴两条渐近线所夹的锐角等于2arctan

故选B.
点评:本小题主要考查双曲线的简单性质、两直线的夹角、直线与圆锥曲线的综合问题等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.

练习册系列答案
相关题目
 已知直线y=-x+1与椭圆
已知直线y=-x+1与椭圆