题目内容
过双曲线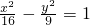 左焦点F1的弦AB长为6,则△ABF2(F2为右焦点)的周长是________.
左焦点F1的弦AB长为6,则△ABF2(F2为右焦点)的周长是________.
28
分析:由双曲线方程求得a=4,由双曲线的定义可得 AF2+BF2 =22,△ABF2的周长是( AF1 +AF2 )+( BF1+BF2 )=(AF2+BF2 )+AB,计算可得答案.
解答:由双曲线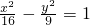 的标准方程可得 a=4,由双曲线的定义可得:
的标准方程可得 a=4,由双曲线的定义可得:
AF2-AF1=2a,BF2 -BF1=2a,
∴AF2+BF2 -AB=4a=16,即AF2+BF2 -6=16,AF2+BF2 =22.
△ABF2(F2为右焦点)的周长是:
( AF1 +AF2 )+( BF1+BF2 )=(AF2+BF2 )+AB=22+6=28.
故答案为:28.
点评:本题考查双曲线的定义的应用,涉及到双曲线上的点和两焦点构成的三角形问题,一般用定义处理.
分析:由双曲线方程求得a=4,由双曲线的定义可得 AF2+BF2 =22,△ABF2的周长是( AF1 +AF2 )+( BF1+BF2 )=(AF2+BF2 )+AB,计算可得答案.
解答:由双曲线
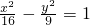 的标准方程可得 a=4,由双曲线的定义可得:
的标准方程可得 a=4,由双曲线的定义可得:AF2-AF1=2a,BF2 -BF1=2a,
∴AF2+BF2 -AB=4a=16,即AF2+BF2 -6=16,AF2+BF2 =22.
△ABF2(F2为右焦点)的周长是:
( AF1 +AF2 )+( BF1+BF2 )=(AF2+BF2 )+AB=22+6=28.
故答案为:28.
点评:本题考查双曲线的定义的应用,涉及到双曲线上的点和两焦点构成的三角形问题,一般用定义处理.

练习册系列答案
相关题目
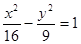 左焦点F1的弦AB长为6,则
左焦点F1的弦AB长为6,则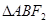 (F2为右焦点)的周长是(
)
(F2为右焦点)的周长是(
)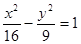 左焦点F1的弦AB长为6,则
左焦点F1的弦AB长为6,则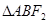 (F2为右焦点)的周长是( )
(F2为右焦点)的周长是( )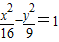 左焦点F1的弦AB长为6,则△ABF2(F2为右焦点)的周长是( )
左焦点F1的弦AB长为6,则△ABF2(F2为右焦点)的周长是( )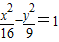 左焦点F1的弦AB长为6,则△ABF2(F2为右焦点)的周长是( )
左焦点F1的弦AB长为6,则△ABF2(F2为右焦点)的周长是( )