题目内容
已知函数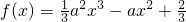 .
.
(I)当a=1时,求函数f(x)在点(1,f(1))的切线方程;
(Ⅱ)求a>2时,函数f(x)在区间(-1,1)上的极值.
解:(I)当a=1时,f(x)= x3-x2+
x3-x2+ ,f′(x)=x2-2x…(2分)
,f′(x)=x2-2x…(2分)
∴k=f′(1)=1-2=-1,f(1)= -1+
-1+ =0,
=0,
∴y-0=-(x-1)
即x+y-1=0为所求切线方程.…(4分)
(II)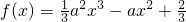 ,f′(x)=a2x2-2ax=a2x(x-
,f′(x)=a2x2-2ax=a2x(x- ),
),
令f'(x)=0得x=0或x= …(6分)
…(6分)
当a>2时,0< <1,
<1,
令f'(x)>0可得x<0或x> ;令f'(x)<0可得0<x<
;令f'(x)<0可得0<x< ,
,
∴f(x)在(-1,0)递增,在(0, )递减,在(
)递减,在( ,1)递增
,1)递增
∴f(x)的极大值为f(0)= ,f(x)的极小值为f(
,f(x)的极小值为f( )=-
)=-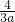 +
+ …(10分)
…(10分)
分析:(I)当a=1时,利用导数的几何意义,确定切线的斜率,求得切点坐标,即可得到切线方程;
(II)当a>2时,求导函数,确定函数的单调性,从而可得函数f(x)的极大值和极小值.
点评:本题考查导数知识的运用,考查函数的单调性与极值,正确求导,恰当计算是关键.
 x3-x2+
x3-x2+ ,f′(x)=x2-2x…(2分)
,f′(x)=x2-2x…(2分)∴k=f′(1)=1-2=-1,f(1)=
 -1+
-1+ =0,
=0,∴y-0=-(x-1)
即x+y-1=0为所求切线方程.…(4分)
(II)
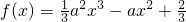 ,f′(x)=a2x2-2ax=a2x(x-
,f′(x)=a2x2-2ax=a2x(x- ),
),令f'(x)=0得x=0或x=
 …(6分)
…(6分)当a>2时,0<
 <1,
<1,令f'(x)>0可得x<0或x>
 ;令f'(x)<0可得0<x<
;令f'(x)<0可得0<x< ,
,∴f(x)在(-1,0)递增,在(0,
 )递减,在(
)递减,在( ,1)递增
,1)递增∴f(x)的极大值为f(0)=
 ,f(x)的极小值为f(
,f(x)的极小值为f( )=-
)=-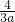 +
+ …(10分)
…(10分)分析:(I)当a=1时,利用导数的几何意义,确定切线的斜率,求得切点坐标,即可得到切线方程;
(II)当a>2时,求导函数,确定函数的单调性,从而可得函数f(x)的极大值和极小值.
点评:本题考查导数知识的运用,考查函数的单调性与极值,正确求导,恰当计算是关键.

练习册系列答案
相关题目
 .
. ,
, .
. 。
。 的解集;
的解集;