题目内容
12.在△ABC中,$\overrightarrow{A{B}^{\;}}$2=$\overrightarrow{BA}$•$\overrightarrow{BC}$,$\overrightarrow{OA}$+$\overrightarrow{OC}$+$\overrightarrow{AB}$=0,且|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|=1,则$\overrightarrow{CA}$•$\overrightarrow{CB}$等于( )| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 2$\sqrt{3}$ |
分析 根据已知条件便知道∠BAC=90°,取AC边的中点D,连接OD,便可得到OD⊥AC,$|\overrightarrow{OD}|=\frac{1}{2}|\overrightarrow{AB}|=\frac{1}{2}$,这时候可以画出图形,结合图形即可求出$|\overrightarrow{CA}|,|\overrightarrow{CB}|$,cos∠BCA,根据向量数量积的计算公式即可求出$\overrightarrow{CA}•\overrightarrow{CB}$.
解答 解:由${\overrightarrow{AB}}^{2}=\overrightarrow{BA}•\overrightarrow{BC}$得$|\overrightarrow{AB}||\overrightarrow{AB}|=|\overrightarrow{BA}||\overrightarrow{BC}|cos∠ABC$;
∴$|\overrightarrow{AB}|=|\overrightarrow{BC}|cos∠ABC$;
∴∠BAC=90°;
由$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{AB}=\overrightarrow{0}$得,$\overrightarrow{OA}+\overrightarrow{OB}=-\overrightarrow{AB}$;
∴$(\overrightarrow{OA}+\overrightarrow{OB})⊥\overrightarrow{AC}$,如图所示: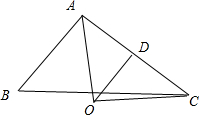 D为AC边中点,$\overrightarrow{OD}=\frac{1}{2}\overrightarrow{BA}$;
D为AC边中点,$\overrightarrow{OD}=\frac{1}{2}\overrightarrow{BA}$;
∴$|\overrightarrow{OD}|=\frac{1}{2}$,$|\overrightarrow{OA}|=1$;
∴$|\overrightarrow{AD}|=\frac{\sqrt{3}}{2}$,$|\overrightarrow{CA}|=\sqrt{3}$;
∴$|\overrightarrow{CB}|=2$,$cos∠BCA=\frac{\sqrt{3}}{2}$;
∴$\overrightarrow{CA}•\overrightarrow{CB}=3$.
故选A.
点评 考查余弦函数的定义,向量数量积的计算公式,以及向量加法的平行四边形法则,直角三角形边角的关系.


| A. | 2 | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{20}{9}$ |
 如图在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,设E、F分别为PC、BD的中点.
如图在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,设E、F分别为PC、BD的中点.