题目内容
在递增等差数列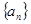
（
）中，已知
，
是
和
的等比中项.
（1）求数列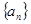的通项公式；
（2）设数列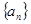的前
项和为
，求使
时的最小值.
【解析】本试题主要考查了数列通项公式的求解以及前n项和公式的运用。并求解最值。
【答案】
（1）解：在递增等差数列
中，设公差为
，
3分
解得
----------6分
--9分
得
故n的最小值为5
练习册系列答案
相关题目
中，
，
成等比数列数列
的前n项和为Sn，且
.
，求数列
的前
和
．
．
，求数列{cn}的前n和Tn．