题目内容
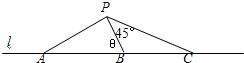 如图,A,B,C是直线l上三点,P是直线l外一点,已知AB=BC=a,∠APB=90°,∠BPC=45°,记∠PBA=θ,则
如图,A,B,C是直线l上三点,P是直线l外一点,已知AB=BC=a,∠APB=90°,∠BPC=45°,记∠PBA=θ,则| PA |
| PC |
分析:三角形ABP是直角三角形,求出|
|、|
|,再有正弦定理求|
|,结合余弦定理,求出θ的余弦值,求数量积即可.
| PA |
| PB |
| PC |
解答:解:|
|=asinθ,|
|=acosθ,|
|=sin(π-θ)
=
asinθ,
且|
|2=|
|2+|
|2-2|
||
|cos(π-θ)=a2+a2cos2θ+2a2cos2θ
=a2+3a2cos2θ,∴2a2sin2θ=a2+3a2cos2θ,
解得sin2θ=
,
则
•
=|
||
|cos135°= -
a2sin2θ
=-
a2,
故答案为:-
a2.
| PA |
| PB |
| PC |
| a |
| sin45° |
| 2 |
且|
| PC |
| PB |
| BC |
| PB |
| BC |
=a2+3a2cos2θ,∴2a2sin2θ=a2+3a2cos2θ,
解得sin2θ=
| 4 |
| 5 |
则
| PA |
| PC |
| PA |
| PC |
| 2 |
| ||
| 2 |
| 4 |
| 5 |
故答案为:-
| 4 |
| 5 |
点评:本题考查平面向量数量积,正弦定理,余弦定理等知识,是综合题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
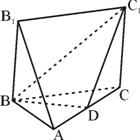
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC, 如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点. 如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=1,O′B′=
如图,△A′B′C′是水平放置的△ABC的斜二测直观图,其中O′C′=O′A′=1,O′B′=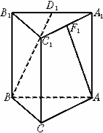
 (1)求证:AB1∥面BDC1;(2)求二面角C-BC1-D的大小;
(1)求证:AB1∥面BDC1;(2)求二面角C-BC1-D的大小;