题目内容
若数列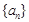 满足:存在正整数
满足:存在正整数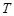 ,对于任意正整数
,对于任意正整数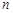 都有
都有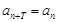 成立,则称数列
成立,则称数列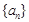 为周期数列,周期为
为周期数列,周期为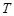 . 已知数列
. 已知数列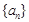 满足
满足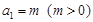 ,
,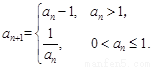
则下列结论中错误的是( )
A. 若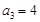 ,则
,则 可以取3个不同的值
可以取3个不同的值
B. 若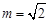 ,则数列
,则数列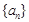 是周期为
是周期为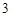 的数列
的数列
C.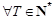 且
且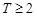 ,存在
,存在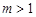 ,
,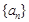 是周期为
是周期为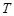 的数列
的数列
D.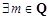 且
且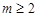 ,数列
,数列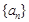 是周期数列
是周期数列
【答案】
D
【解析】
试题分析:当 时,有
时,有 或
或 ,从而有:
,从而有: 或
或 .同理:由
.同理:由 可得:
可得: 或
或 即:
即: 或
或 ;由
;由 可得:
可得: 或
或 ,即
,即 .综上可知,
.综上可知, 可取
可取 三个不同的值,故A中的结论是正确的;当
三个不同的值,故A中的结论是正确的;当 时,
时, ,
, ,
, ……,数列
……,数列 是周期为3的数列,故B中的结论是正确的,C由B可知,当
是周期为3的数列,故B中的结论是正确的,C由B可知,当 时,数列
时,数列 是周期为3的数列,所以C正确.由以上可知,四个选项中,结论错误的为D.
是周期为3的数列,所以C正确.由以上可知,四个选项中,结论错误的为D.
考点:分段函数、周期数列.

练习册系列答案
相关题目

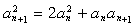
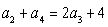
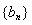
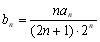
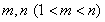
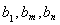
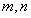
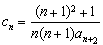
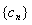
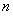
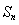
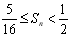
 满足
满足 ,且
,且 ,其中
,其中 .
. 满足
满足 是否存在正整数m、n(1<m<n),使得
是否存在正整数m、n(1<m<n),使得 成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。
成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。 满足:存在正整数
满足:存在正整数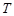 ,对于任意正整数
,对于任意正整数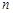 都有
都有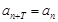 成立,则称数列
成立,则称数列 ,
,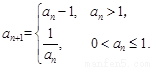
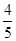 ,则a5=3
,则a5=3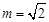 ,则数列
,则数列 的数列
的数列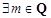 且
且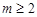 ,数列
,数列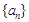 是周期数列
是周期数列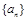 的前
的前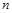 项和
项和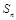 和通项
和通项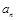 满足
满足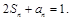 数列
数列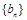 中,
中,
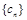 满足
满足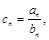 是否存在正整数
是否存在正整数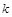 ,使得
,使得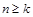 时
时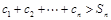 恒成立?若存在,求
恒成立?若存在,求