Question

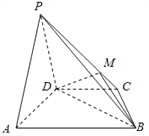
【题目】在如图所示的三棱锥中，底面分别是的中点．

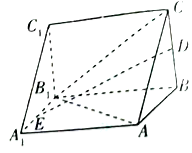
（1）求证：平面；

（2）若，求直线与平面所成角的正切值．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

试题分析：（1）借助题设条件运用线面平行的判定定理求解；（2）借助题设运用直线与平面所成角的定义找出其角,再运用解三角形的方法求解.

试题解析：（1）取的中点，连接

在中，因为分别为的中点，

所以平面平面，

所以平面

在矩形中，因为分别为的中点，

所以平面 平面，所以平面

因为，所以平面平面

因为平面，所以平面

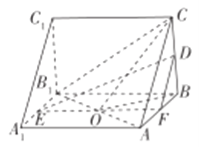
（2）因为三棱柱为直三棱柱，所以，

又，所以平面，

因为，所以，

又，所以为正三角形，

所以，所以

取的中点，连接，所以，所以平面，

所以平面平面，点在平面上的射影在上，

所以即为直线与平面所成角

在中，，所以．．．．．．．．．12分

（若用空间向量处理，请相应给分）