题目内容
1.己知定义在R上的奇函数f(x)的图象为一条连续不断的曲线,f(1+x)=f(1-x),f(1)=a,且0<x<1时,f(x)的导函数f′(x)满足:f′(x)<f(x),则f(x)在[2015,2016]上的最大值为-a.分析 由题意求出函数的周期,根据函数的周期性求出函数在[2015,2016]的单调性,转化f(2015)=-f(1),从而求出函数的闭区间上的最大值即可.
解答 解:∵己知定义在R上的奇函数f(x)的图象为一条连续不断的曲线,
∴f(-x)=-f(x),
∵f(x+1)=f(1-x),
∴f(x+2)=f[(x+1)+1]=f[1-(x+1)]=f(-x)=-f(x),
即f(x+2)=-f(x),
f(x+4)=-f(x+2),
∴f(x+4)=f(x),
∴函数的周期为4,
0<x<1时,f(x)的导函数f′(x)满足:f′(x)<0,
∴f(x)在(0,1)递减,f(x)在[2015,2016]递减,
∴f(2015)=f(4×504-1)=f(-1)=-f(1),
∵f(1)=a,
∴f(2015)=-f(1)=-a,
故f(x)在[2015,2016]上的最大值为为:f(2015)=-a,
故答案为:-a.
点评 本题考查函数的奇偶性、周期性的应用,函数值的求法以及函数的单调性问题,考查计算能力,是一道中档题.

练习册系列答案
相关题目
11.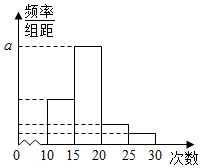 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(1)求出表中M、p及图中a的值;
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间[20,25)内的概率.
 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
(2)试估计他们参加社区服务的平均次数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至少1人参加社区服务次数在区间[20,25)内的概率.
11.已知tan2θ=$\frac{3}{4}$,θ∈(0,$\frac{π}{4}$),则$\frac{si{n}^{2}θ+cos2θ}{sin(θ+\frac{π}{4})}$的值为( )
| A. | $\frac{9\sqrt{5}}{20}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{10}}{3}$ | D. | $\frac{\sqrt{10}}{10}$ |