题目内容
函数f(x)=sin2x+2 cos2x-
cos2x- ,函数g(x)=mcos(2x-
,函数g(x)=mcos(2x- )-2m+3(m>0),若存在x1,x2
)-2m+3(m>0),若存在x1,x2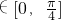 ,使得f(x1)=g(x2)成立,则实数m的取值范围是________.
,使得f(x1)=g(x2)成立,则实数m的取值范围是________.
[ ,2]
,2]
分析:由x∈[0, ],可求得f(x)∈[1,2],g(x)∈[-
],可求得f(x)∈[1,2],g(x)∈[-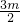 +3,3-m],依题意,存在x1,x2
+3,3-m],依题意,存在x1,x2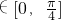 ,使得f(x1)=g(x2)成立,可得到关于m的不等式组,解之可求得实数m的取值范围.
,使得f(x1)=g(x2)成立,可得到关于m的不等式组,解之可求得实数m的取值范围.
解答:∵f(x)=sin2x+2 cos2x-
cos2x- =sin2x+
=sin2x+ cos2x=2sin(2x+
cos2x=2sin(2x+ ),
),
当x∈[0, ],2x+
],2x+ ∈[
∈[ ,
, ],
],
∴sin(2x+ )∈[1,2],
)∈[1,2],
∴f(x)∈[1,2],
对于g(x)=mcos(2x- )-2m+3(m>0),2x-
)-2m+3(m>0),2x- ∈[-
∈[- ,
, ],mcos(2x-
],mcos(2x- )∈[
)∈[ ,m],
,m],
∴g(x)∈[-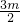 +3,3-m],
+3,3-m],
若存在x1,x2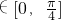 ,使得f(x1)=g(x2)成立,
,使得f(x1)=g(x2)成立,
则3-m≥1,-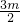 +3≤2,解得实数m的取值范围是[
+3≤2,解得实数m的取值范围是[ ,2].
,2].
故答案为:[ ,2].
,2].
点评:本题考查两角和与差的正弦函数,着重考查三角函数的性质的运用,考查二倍角的余弦,解决问题的关键是理解“存在x1,x2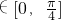 ,使得f(x1)=g(x2)成立”的含义,属于难题.
,使得f(x1)=g(x2)成立”的含义,属于难题.
 ,2]
,2]分析:由x∈[0,
 ],可求得f(x)∈[1,2],g(x)∈[-
],可求得f(x)∈[1,2],g(x)∈[-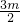 +3,3-m],依题意,存在x1,x2
+3,3-m],依题意,存在x1,x2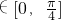 ,使得f(x1)=g(x2)成立,可得到关于m的不等式组,解之可求得实数m的取值范围.
,使得f(x1)=g(x2)成立,可得到关于m的不等式组,解之可求得实数m的取值范围.解答:∵f(x)=sin2x+2
 cos2x-
cos2x- =sin2x+
=sin2x+ cos2x=2sin(2x+
cos2x=2sin(2x+ ),
),当x∈[0,
 ],2x+
],2x+ ∈[
∈[ ,
, ],
],∴sin(2x+
 )∈[1,2],
)∈[1,2],∴f(x)∈[1,2],
对于g(x)=mcos(2x-
 )-2m+3(m>0),2x-
)-2m+3(m>0),2x- ∈[-
∈[- ,
, ],mcos(2x-
],mcos(2x- )∈[
)∈[ ,m],
,m],∴g(x)∈[-
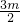 +3,3-m],
+3,3-m],若存在x1,x2
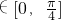 ,使得f(x1)=g(x2)成立,
,使得f(x1)=g(x2)成立,则3-m≥1,-
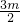 +3≤2,解得实数m的取值范围是[
+3≤2,解得实数m的取值范围是[ ,2].
,2].故答案为:[
 ,2].
,2].点评:本题考查两角和与差的正弦函数,着重考查三角函数的性质的运用,考查二倍角的余弦,解决问题的关键是理解“存在x1,x2
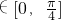 ,使得f(x1)=g(x2)成立”的含义,属于难题.
,使得f(x1)=g(x2)成立”的含义,属于难题. 
练习册系列答案
相关题目
 函数f(x)=sin(ωx+?)(x∈R,ω>0,0≤?<2π)的部分图象如图,则
函数f(x)=sin(ωx+?)(x∈R,ω>0,0≤?<2π)的部分图象如图,则