题目内容
在△ABC中,若lgsinA-lgcosB-lgsinC=lg2,则△ABC的形状是( )A.直角三角形
B.等边三角形
C.不能确定
D.等腰三角形
【答案】分析:利用对数的运算法则可求得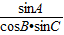 =2,利用正弦定理求得cosB,同时根据余弦定理求得cosB的表达式进而建立等式,整理求得b=c,判断出三角形为等腰三角形.
=2,利用正弦定理求得cosB,同时根据余弦定理求得cosB的表达式进而建立等式,整理求得b=c,判断出三角形为等腰三角形.
解答:解:∵lgsinA-lgcosB-lgsinC=lg2,
∴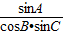 =2,
=2,
由正弦定理可知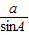 =
=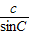
∴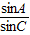 =
=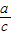
∴cosB=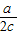 ,
,
∴cosB=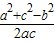 =
=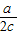 ,
,
整理得c=b,
∴△ABC的形状是等腰三角形.
故选D
点评:本题主要考查了正弦定理和余弦定理的应用.解题的关键是利用正弦定理和余弦定理完成了边角问题的互化.
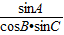 =2,利用正弦定理求得cosB,同时根据余弦定理求得cosB的表达式进而建立等式,整理求得b=c,判断出三角形为等腰三角形.
=2,利用正弦定理求得cosB,同时根据余弦定理求得cosB的表达式进而建立等式,整理求得b=c,判断出三角形为等腰三角形.解答:解:∵lgsinA-lgcosB-lgsinC=lg2,
∴
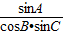 =2,
=2,由正弦定理可知
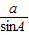 =
=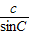
∴
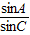 =
=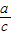
∴cosB=
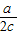 ,
,∴cosB=
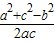 =
=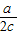 ,
,整理得c=b,
∴△ABC的形状是等腰三角形.
故选D
点评:本题主要考查了正弦定理和余弦定理的应用.解题的关键是利用正弦定理和余弦定理完成了边角问题的互化.

练习册系列答案
相关题目
在锐角△ABC中,若lg (1+sinA)=m,且lg
=n,则lgcosA等于( )
| 1 |
| 1-sinA |
A、
| ||||
| B、m-n | ||||
C、
| ||||
D、m+
|