题目内容
已知-1<a,b,c<1,比较ab+bc+ca与-1的大小关系为
>
>
.分析:根据题意可得:设f(x)=(b+c)x+bc+1,并且f(x)是单调函数,结合条件可得f(1)>0,f(-1)>0,进而得到-1<x<1时,有f(x)>0恒成立,则有f(a)=(b+c)a+bc+1>0,进而得到答案.
解答:解:根据题意可得:设f(x)=(b+c)x+bc+1,
由函数的性质可得:f(x)是单调函数,
因为f(1)=(1+b)(1+c)>0,f(-1)=(-1+b)(-1+c)=(1-b)(1-c)>0,
所以-1<x<1时,有f(x)>0恒成立,
所以f(a)=(b+c)a+bc+1>0,即ab+bc+ca>-1.
故答案为:>.
由函数的性质可得:f(x)是单调函数,
因为f(1)=(1+b)(1+c)>0,f(-1)=(-1+b)(-1+c)=(1-b)(1-c)>0,
所以-1<x<1时,有f(x)>0恒成立,
所以f(a)=(b+c)a+bc+1>0,即ab+bc+ca>-1.
故答案为:>.
点评:解决此类问题的关键是熟练掌握函数的单调性,以及利用函数的单调性比较大小,考查学生构造函数的能力,以及分析问题、解决问题的能力.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
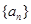 是由正数组成的等比数列,
是由正数组成的等比数列,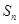 为数列的前
为数列的前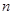 项的和,已知
项的和,已知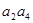 =1,
=1,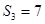 ,则
,则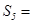
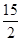 B.
B.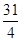 C.
C.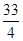 D.
D.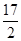
 }是由正数组成的等比数列,
}是由正数组成的等比数列, 为其前n项和。已知
为其前n项和。已知
 =1,
=1,  ,则
,则 ( )
( ) B.
B. C.
C. D.
D.