题目内容
已知点p（x，y）在椭圆
上，则x2+2x-y2的最大值为________．
8
分析：利用椭圆方程，化代数式二元为一元，根据椭圆方程确定变量范围，利用配方法，即可求得结论．
解答：∵，∴
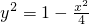
由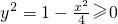
可得-2≤x≤2
又x2+2x-y2=
x2+2x-1=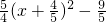
∵-2≤x≤2
∴x=2时，函数取得最大值8，即x2+2x-y2的最大值为8
故答案为：8
点评：本题考查求最大值，考查学生转化问题的能力，考查学生的计算，属于中档题．
分析：利用椭圆方程，化代数式二元为一元，根据椭圆方程确定变量范围，利用配方法，即可求得结论．
解答：∵
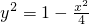
，∴由
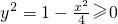可得-2≤x≤2又x2+2x-y2=
x2+2x-1=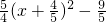∵-2≤x≤2
∴x=2时，函数取得最大值8，即x2+2x-y2的最大值为8
故答案为：8
点评：本题考查求最大值，考查学生转化问题的能力，考查学生的计算，属于中档题．
练习册系列答案
轻松暑假总复习系列答案
相关题目