题目内容
已知曲线C:y=x2(x>0),过C上的点A1(1,1)作曲线C的切线l1交x轴于点B1,再过B1作y轴的平行线交曲线C于点A2,再过A2作曲线C的切线l2交x轴于点B2,再过B2作y轴的平行线交曲线C于点A&3,…,依次作下去,记点An的横坐标为an(n∈N*).(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记bn=(8-2n)an,设数列{bn}的前n项和为Tn,求证:0<Tn≤4.
【答案】分析:(I)由y'=2x(x>0).知切线ln的方程为y-an2=2an(x-an).所以 .依题意点An+1在直线
.依题意点An+1在直线 上,所以数列{an}是1为首项,
上,所以数列{an}是1为首项, 为公比的等比数列.由此能求出数列{an}的通项公式.
为公比的等比数列.由此能求出数列{an}的通项公式.
(Ⅱ)由 ,知
,知 .由错位相减法能导出
.由错位相减法能导出 ,n≥2时,
,n≥2时,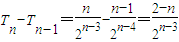 .由n≥2时,Tn≤Tn-1,知Tn≤Tn-1≤…≤T2,由此能够证明0<Tn≤4.
.由n≥2时,Tn≤Tn-1,知Tn≤Tn-1≤…≤T2,由此能够证明0<Tn≤4.
解答:解(I)∵y'=2x(x>0).∴曲线C在点An(an,an2)处的切线ln的斜率为kn=2an.
∴切线ln的方程为y-an2=2an(x-an).(2分)
令y=0得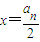 ,
,
∴ .
.
依题意点An+1在直线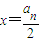 上,
上,
∴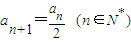 又a1=1.(4分)
又a1=1.(4分)
∴数列{an}是1为首项, 为公比的等比数列.
为公比的等比数列.
∴ .(5分)
.(5分)
(Ⅱ)由已知 .
.
∴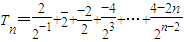 .①
.①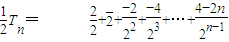 .②
.②
①-②得 =
= =
= .(9分)
.(9分)
∴ (10分)
(10分)
又n≥2时, .
.
又当n≥2时,Tn≤Tn-1.
∴Tn≤Tn-1≤…≤T2.
∴当n=2时,T1=T2=4.
∴(Tn)max=T2=4,∴Tn≤4.(13分)
综上0<Tn≤4.(14分)
点评:本题考查通项公式的求法和求证:0<Tn≤4.解题时要认真审题,仔细解答,注意合理地进行等价转化.
 .依题意点An+1在直线
.依题意点An+1在直线 上,所以数列{an}是1为首项,
上,所以数列{an}是1为首项, 为公比的等比数列.由此能求出数列{an}的通项公式.
为公比的等比数列.由此能求出数列{an}的通项公式.(Ⅱ)由
 ,知
,知 .由错位相减法能导出
.由错位相减法能导出 ,n≥2时,
,n≥2时,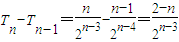 .由n≥2时,Tn≤Tn-1,知Tn≤Tn-1≤…≤T2,由此能够证明0<Tn≤4.
.由n≥2时,Tn≤Tn-1,知Tn≤Tn-1≤…≤T2,由此能够证明0<Tn≤4.解答:解(I)∵y'=2x(x>0).∴曲线C在点An(an,an2)处的切线ln的斜率为kn=2an.
∴切线ln的方程为y-an2=2an(x-an).(2分)
令y=0得
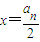 ,
,∴
 .
.依题意点An+1在直线
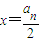 上,
上,∴
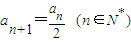 又a1=1.(4分)
又a1=1.(4分)∴数列{an}是1为首项,
 为公比的等比数列.
为公比的等比数列.∴
 .(5分)
.(5分)(Ⅱ)由已知
 .
.∴
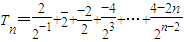 .①
.①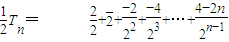 .②
.②①-②得
 =
= =
= .(9分)
.(9分)∴
 (10分)
(10分)又n≥2时,
 .
.又当n≥2时,Tn≤Tn-1.
∴Tn≤Tn-1≤…≤T2.
∴当n=2时,T1=T2=4.
∴(Tn)max=T2=4,∴Tn≤4.(13分)
综上0<Tn≤4.(14分)
点评:本题考查通项公式的求法和求证:0<Tn≤4.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.
如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y 轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.