题目内容
已知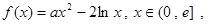 (其中
(其中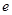 是自然对数的底)
是自然对数的底)
(1) 若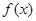 在
在 处取得极值,求
处取得极值,求 的值;
的值;
(2) 若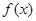 存在极值,求a的取值范围
存在极值,求a的取值范围
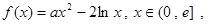 (其中
(其中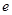 是自然对数的底)
是自然对数的底)(1) 若
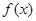 在
在 处取得极值,求
处取得极值,求 的值;
的值;(2) 若
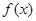 存在极值,求a的取值范围
存在极值,求a的取值范围(1) 1;(2)

试题分析:(1) 首先求出
 ,再根据若
,再根据若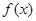 在
在 处取得极值的条件求出
处取得极值的条件求出 的值;
的值;(2)由
 =
= ,把函数的极值存在性问题转化为关于
,把函数的极值存在性问题转化为关于 的方程在
的方程在 内有解的问题即可.
内有解的问题即可.试题解析:


因为
 在
在 处取得极值
处取得极值所以,
 ,即:
,即:
所以,

(2)由(1)知:

因为
 ,
,
当
 时,
时, 在
在 上恒成立,
上恒成立, 在
在 是减函数,无极值;
是减函数,无极值;当
 时,
时, 在
在 上恒成立,
上恒成立, 在
在 是减函数,无极值;
是减函数,无极值;当
 时,
时, 的减区间是
的减区间是 ,增区间是
,增区间是 .此时
.此时 有极值.
有极值.
练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
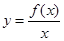 在
在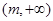 上为增函数(
上为增函数( 为常数),则称
为常数),则称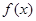 为区间
为区间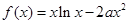 是
是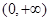 上的“一阶比增函数”,求实数
上的“一阶比增函数”,求实数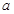 的取值范围;
的取值范围;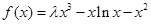 (
(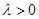 ,
,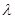 为常数),且
为常数),且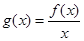 有唯一的零点,求
有唯一的零点,求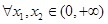 ,
,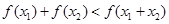
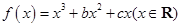 ,若
,若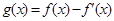 是奇函数,则
是奇函数,则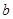 +
+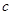 的值为
的值为  在区间
在区间 上有极值点,则实数
上有极值点,则实数 的取值范围是( )
的取值范围是( )


