题目内容
在数列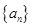 中,
中,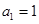 ,
,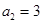 ,
,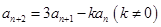 对任意
对任意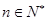 成立,令
成立,令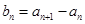 ,且
,且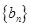 是等比数列.
是等比数列.
(1)求实数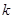 的值;
的值;
(2)求数列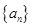 的通项公式;
的通项公式;
(3)求证: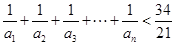 .
.
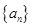 中,
中,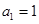 ,
,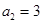 ,
,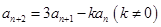 对任意
对任意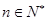 成立,令
成立,令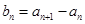 ,且
,且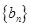 是等比数列.
是等比数列.(1)求实数
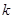 的值;
的值;(2)求数列
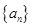 的通项公式;
的通项公式;(3)求证:
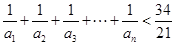 .
.(1) ;(2)
;(2) ;(3)详见解析.
;(3)详见解析.
 ;(2)
;(2) ;(3)详见解析.
;(3)详见解析.试题分析:(1)先利用题中的定义,利用数列
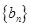 的前三项成等比数列求出
的前三项成等比数列求出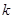 的值,然后就
的值,然后就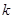 的值进行检验,即对数列
的值进行检验,即对数列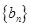 是否为等比数列进行检验;(2)根据等比数列
是否为等比数列进行检验;(2)根据等比数列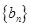 的通项
的通项 选择累加法求数列
选择累加法求数列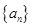 的通项公式;(3)利用
的通项公式;(3)利用 ,将数列
,将数列 从第三项开始放缩为一个等比数列,而前面两项的值保持不变,再利用数列求和即可证明相应的数列不等式.
从第三项开始放缩为一个等比数列,而前面两项的值保持不变,再利用数列求和即可证明相应的数列不等式.试题解析:(1)
 ,
,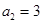 ,
, ,
, ,
, ,
, ,
, ,
, 数列
数列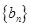 为等比数列,
为等比数列, ,即
,即 ,解得
,解得 或
或 (舍),
(舍),当
 时,
时, ,即
,即 ,
, ,所以
,所以 满足条件;
满足条件;(2)
 ,数列
,数列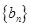 为等比数列,
为等比数列, ,
, ,
, ,
, ,
, ,
, ,
, ;
;(3)
 ,
, ,
,
 .
.
练习册系列答案
相关题目
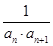 ,其前n项和为Sn.
,其前n项和为Sn.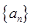 的前
的前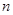 项和为
项和为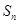 ,
,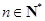 ,且
,且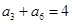 ,
,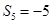 .
.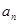 ;
;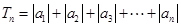 ,求
,求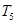 的值和
的值和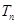 的表达式.
的表达式.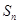 为数列
为数列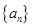 的前
的前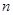 项和,对任意的
项和,对任意的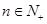 ,都有
,都有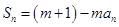 (
(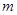 为正常数).
为正常数).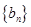 满足
满足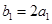 ,
,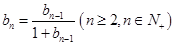 ,求数列
,求数列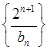 的前
的前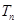 .
.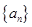 中,
中,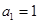 ,
,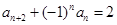 ,记
,记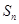 是数列
是数列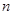 项和,则
项和,则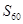 = .
= . 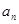 }的前n项和为
}的前n项和为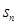 ,若
,若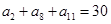 ,那么
,那么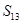 = .
= .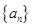 的首项及公差均是正整数,前
的首项及公差均是正整数,前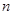 项和为
项和为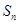 ,且
,且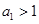 ,
,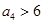 ,
,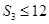 ,则
,则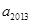 =
= 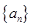 中,
中,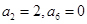 且数列
且数列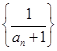 是等差数列,则
是等差数列,则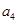 =( )
=( )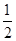
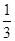
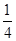
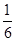
 的通项公式
的通项公式 ,记
,记 ,试计算
,试计算 ,推测
,推测 .
.