题目内容
函数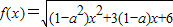 .
.(1)若f(x)的定义域为R,求实数a的取值范围;
(2)若f(x)的定义域为[-2,1],求实数a的值.
【答案】分析:(1)要使f(x)的定义域为R,只需(1-a2)x2+3(1-a)x+6≥0在R上恒成立,然后讨论二次项系数可求出所求;
(2)根据f(x)的定义域为[-2,1]可知(1-a2)x2+3(1-a)x+6≥0的解集为[-2,1],则(1-a2)x2+3(1-a)x+6=0的两个根为-2,1,然后利用根与系数的关系解之即可.
解答:解:(1)∵f(x)的定义域为R,
∴(1-a2)x2+3(1-a)x+6≥0在R上恒成立
当a=1时,6≥0恒成立
当a=-1时,6x+6≥0在R上不恒成立,故舍去
当a≠±1时,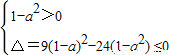
解得:-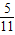 ≤a<1
≤a<1
综上所述:-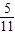 ≤a≤1
≤a≤1
(2)∵f(x)的定义域为[-2,1],
∴(1-a2)x2+3(1-a)x+6≥0的解集为[-2,1],
即(1-a2)x2+3(1-a)x+6=0的两个根为-2,1
∴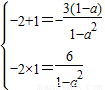 解得a=2
解得a=2
故a的值为2.
点评:本题主要考查了一元二次不等式的应用,以及根与系数的关系和恒成立问题,同时考查了转化的思想和计算的能力,属于中档题.
(2)根据f(x)的定义域为[-2,1]可知(1-a2)x2+3(1-a)x+6≥0的解集为[-2,1],则(1-a2)x2+3(1-a)x+6=0的两个根为-2,1,然后利用根与系数的关系解之即可.
解答:解:(1)∵f(x)的定义域为R,
∴(1-a2)x2+3(1-a)x+6≥0在R上恒成立
当a=1时,6≥0恒成立
当a=-1时,6x+6≥0在R上不恒成立,故舍去
当a≠±1时,
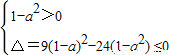
解得:-
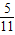 ≤a<1
≤a<1综上所述:-
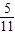 ≤a≤1
≤a≤1(2)∵f(x)的定义域为[-2,1],
∴(1-a2)x2+3(1-a)x+6≥0的解集为[-2,1],
即(1-a2)x2+3(1-a)x+6=0的两个根为-2,1
∴
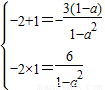 解得a=2
解得a=2故a的值为2.
点评:本题主要考查了一元二次不等式的应用,以及根与系数的关系和恒成立问题,同时考查了转化的思想和计算的能力,属于中档题.

练习册系列答案
相关题目