题目内容
（A）．（选修4—4坐标系与参数方程）已知点
是曲线
上任意一点，
则点到直线
的距离的最小值是 .
是曲线上任意一点，则点
到直线的距离的最小值是 .2
由于直角△ABC的内切圆与斜边AB相切于点D，且AD=1，BD=2，设内切圆半径为r，
则由勾股定理可得（1+r）2+（2+r）2=9，∴r2+3r=2．
△ABC的面积为
×（1+r）（2+r）=（r2+3r+2）=2，
故答案为 2．
则由勾股定理可得（1+r）2+（2+r）2=9，∴r2+3r=2．
△ABC的面积为
×（1+r）（2+r）=（r2+3r+2）=2，故答案为 2．
练习册系列答案
相关题目
中，曲线
的参数方程为
，（其中
为参数，
），在极坐标系（以坐标原点
为极点，以
轴非负半轴为极轴）中，曲线
的极坐标方程为
．
和
，求曲线
的参数方程为
，直线
的极坐标方程为
，则曲线
恒成立，则实数
的取值范围为 .
与曲线
相交，则
的取值范围是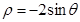 
的圆心的极坐标是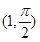
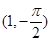
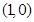
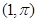
的极坐标方程分别为
，求点C到直线
与曲线
：
的关系是 。
的极坐标方程为
，写出曲线
），则过点P且垂直极轴的直线方程是（ ）
