题目内容
在△ABC中,A=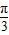 ,BC=2
,BC=2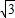 ,设内角B=x,△ABC的面积为y,
,设内角B=x,△ABC的面积为y,(1)求函数y=f(x)的解析式和定义域;
(2)求y的最大值.
【答案】分析:(1)由A与B的度数,利用内角和定理表示出C,求出x的范围即为y=f(x)的定义域,利用正弦定理表示出AB,利用三角形的面积公式列出函数解析式即可;
(2)函数解析式利用两角和与差的正弦函数公式化简,整理后利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域即可确定出y的最大值.
解答:解:(1)△ABC的内角和A+B+C=π,
∵A=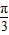 ,B=x,B>0,C>0,
,B=x,B>0,C>0,
∴C=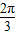 -x,0<x<
-x,0<x<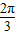 ,即函数y=f(x)的定义域为(0,
,即函数y=f(x)的定义域为(0,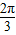 );
);
由正弦定理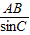 =
=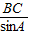 ,得AB=
,得AB=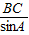 sinC=4sin(
sinC=4sin(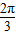 -x),
-x),
∴y= AB•BCsinB=4
AB•BCsinB=4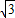 sinxsin(
sinxsin(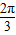 -x)(0<x<
-x)(0<x<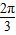 );
);
(2)y=4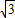 sinxsin(
sinxsin(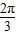 -x)=4
-x)=4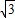 sinx(
sinx(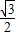 cosx+
cosx+ sinx)=6sinxcosx+2
sinx)=6sinxcosx+2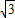 sin2x=3sin2x-
sin2x=3sin2x-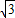 cos2x+
cos2x+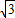 =2
=2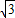 sin(2x-
sin(2x-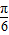 )+
)+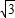 (-
(-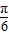 <2x-
<2x-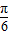 <
<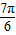 ),
),
当2x-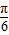 =
=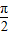 ,即x=
,即x=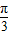 时,y取最大值3
时,y取最大值3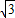 .
.
点评:此题考查了正弦定理,两角和与差的正弦函数公式,二倍角的正弦、余弦函数公式,以及正弦函数的定义域与值域,熟练掌握定理及公式是解本题的关键.
(2)函数解析式利用两角和与差的正弦函数公式化简,整理后利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域即可确定出y的最大值.
解答:解:(1)△ABC的内角和A+B+C=π,
∵A=
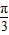 ,B=x,B>0,C>0,
,B=x,B>0,C>0,∴C=
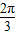 -x,0<x<
-x,0<x<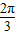 ,即函数y=f(x)的定义域为(0,
,即函数y=f(x)的定义域为(0,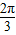 );
);由正弦定理
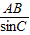 =
=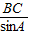 ,得AB=
,得AB=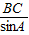 sinC=4sin(
sinC=4sin(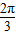 -x),
-x),∴y=
 AB•BCsinB=4
AB•BCsinB=4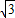 sinxsin(
sinxsin(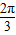 -x)(0<x<
-x)(0<x<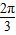 );
);(2)y=4
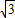 sinxsin(
sinxsin(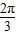 -x)=4
-x)=4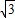 sinx(
sinx(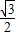 cosx+
cosx+ sinx)=6sinxcosx+2
sinx)=6sinxcosx+2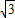 sin2x=3sin2x-
sin2x=3sin2x-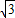 cos2x+
cos2x+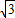 =2
=2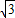 sin(2x-
sin(2x-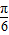 )+
)+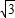 (-
(-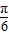 <2x-
<2x-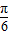 <
<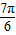 ),
),当2x-
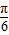 =
=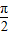 ,即x=
,即x=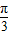 时,y取最大值3
时,y取最大值3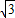 .
.点评:此题考查了正弦定理,两角和与差的正弦函数公式,二倍角的正弦、余弦函数公式,以及正弦函数的定义域与值域,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目