题目内容
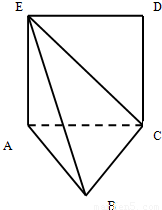
如图，正方形ACDE与△ACB所在的平面互相垂直，且AC=BC，∠ACB=90°，F，G分别是线段AE，BC的中点，则AD与FG所成的角的余弦值为
| ||
| 6 |
| ||
| 6 |
分析：根据题意，建立如图所示空间直角坐标系，设AC=BC=2，可得向量
、
的坐标，利用空间向量的夹角公式加以计算，即可得到异面直线AD与FG所成的角的余弦值．
| AD |
| GF |
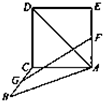
解答：解：
根据题意，分别以CB、CA、CD所在直线为x轴、y轴、z轴，建立空间直角坐标系，如图所示
设AC=BC=2，可得A（0，2，0），D（0，0，2），
G（1，0，0），F（0，2，1），
∴
=（0，-2，2），
=（-1，2，1），
设AD与FG所成的角大小为α，则
cosα=|cos＜
，
＞|=
=
=
，
即AD与FG所成的角的余弦值为
．
故答案为：
根据题意，分别以CB、CA、CD所在直线为x轴、y轴、z轴，建立空间直角坐标系，如图所示设AC=BC=2，可得A（0，2，0），D（0，0，2），
G（1，0，0），F（0，2，1），
∴
| AD |
| GF |
设AD与FG所成的角大小为α，则
cosα=|cos＜
| AD |
| GF |
|
| ||||
|
=
| |0×(-1)+(-2)×2+2×1| | ||||
|
| ||
| 6 |
即AD与FG所成的角的余弦值为
| ||
| 6 |
故答案为：
| ||
| 6 |
点评：本题给出正方形所在平面与直角三角形所在平面互相垂直，求面直线AD与FG所成的角的余弦值．着重考查了面面垂直的性质和利用空间向量研究异面直线所成角大小等知识，属于中档题．
练习册系列答案
相关题目
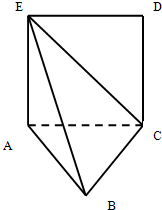如图，正方形ACDE边长为1且所在的平面与平面ABC垂直，AC⊥BC，且AC=BC．
（2010•衡阳模拟）如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，AC⊥BC，且AC=BC．
