题目内容
在△ABC中,已知AB=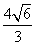 ,cosB=
,cosB=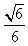 ,AC边上的中线BD=
,AC边上的中线BD=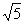 ,求sinA的值。
,求sinA的值。
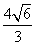 ,cosB=
,cosB=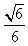 ,AC边上的中线BD=
,AC边上的中线BD=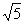 ,求sinA的值。
,求sinA的值。解:设E为BC的中点,连接DE,则DE∥AB,且DE=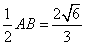 ,
,
设BE=x,
在△BDE中利用余弦定理可得:BD2=BE2+ED2-2BE·EDcos∠BED,
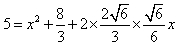 ,
,
解得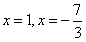 (舍去),
(舍去),
故BC=2,
从而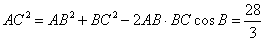 ,
,
即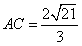 ,
,
又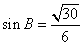 ,
,
故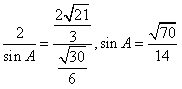 。
。
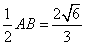 ,
,设BE=x,
在△BDE中利用余弦定理可得:BD2=BE2+ED2-2BE·EDcos∠BED,
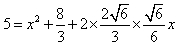 ,
,解得
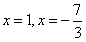 (舍去),
(舍去),故BC=2,
从而
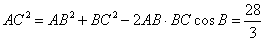 ,
,即
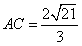 ,
,又
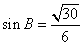 ,
,故
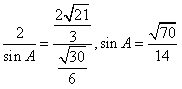 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目