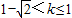题目内容
若对任意实数x,cos2x+2ksinx-2k-2<0恒成立,则实数k的取值范围是
- A.
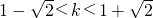
- B.
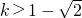
- C.
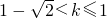
- D.k>-1
B
分析:根据同角三角函数的关系,我们可将不等式转化为2k>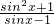 恒成立,求出
恒成立,求出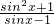 的最大值,即可得到答案.
的最大值,即可得到答案.
解答:∵cos2x+2ksinx-2k-2=1-sin2x+2ksinx-2k-2=-sin2x+2ksinx-2k-1=2k(sinx-1)-(sin2x+1)<0恒成立
即2k(sinx-1)<(sin2x+1)恒成立
当sinx-1=0时,显然成立
当sinx-1≠0时,则sinx-1<0
故2k>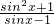 恒成立
恒成立
令t=sinx,y=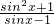 =
=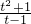 (-1≤t<1)
(-1≤t<1)
则y′=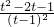
令y′=0,则t2-2t-1=0,
解得t=1- ,或t=1+
,或t=1+ (舍去)
(舍去)
由t∈[-1,1- )时,y′>0,t∈(1-
)时,y′>0,t∈(1- ,1)时,y′<0,
,1)时,y′<0,
∴y=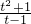 (-1≤t<1)在[-1,1-
(-1≤t<1)在[-1,1- )上递增;在(1-
)上递增;在(1- ,1)上递减
,1)上递减
即ymax=y|t=1 =2-2
=2-2
则2k>2-2
则k>1-
故选B
点评:本题考查的知识点是函数恒成立问题,将其转化为最值问题是解答的关键.
分析:根据同角三角函数的关系,我们可将不等式转化为2k>
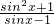 恒成立,求出
恒成立,求出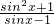 的最大值,即可得到答案.
的最大值,即可得到答案.解答:∵cos2x+2ksinx-2k-2=1-sin2x+2ksinx-2k-2=-sin2x+2ksinx-2k-1=2k(sinx-1)-(sin2x+1)<0恒成立
即2k(sinx-1)<(sin2x+1)恒成立
当sinx-1=0时,显然成立
当sinx-1≠0时,则sinx-1<0
故2k>
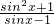 恒成立
恒成立令t=sinx,y=
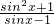 =
=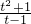 (-1≤t<1)
(-1≤t<1)则y′=
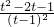
令y′=0,则t2-2t-1=0,
解得t=1-
 ,或t=1+
,或t=1+ (舍去)
(舍去)由t∈[-1,1-
 )时,y′>0,t∈(1-
)时,y′>0,t∈(1- ,1)时,y′<0,
,1)时,y′<0,∴y=
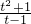 (-1≤t<1)在[-1,1-
(-1≤t<1)在[-1,1- )上递增;在(1-
)上递增;在(1- ,1)上递减
,1)上递减即ymax=y|t=1
 =2-2
=2-2
则2k>2-2

则k>1-

故选B
点评:本题考查的知识点是函数恒成立问题,将其转化为最值问题是解答的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
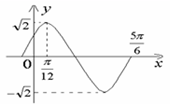 函数
函数