题目内容
M(2,-3),N(-3,-2)直线l过点P(1,1)且与线段MN相交,则l的斜率k的取值范围为( )
A、k≠-
| ||
B、-4≤k≤
| ||
C、k≤-4或k≥
| ||
D、-
|
分析:画出图形,由题意得 所求直线l的斜率k满足 k≥kPB 或 k≤kPA,用直线的斜率公式求出kPB 和kPA 的值,
解不等式求出直线l的斜率k的取值范围.
解不等式求出直线l的斜率k的取值范围.
解答: 解:如图所示:由题意得,所求直线l的斜率k满足 k≥kPB 或 k≤kPA,
解:如图所示:由题意得,所求直线l的斜率k满足 k≥kPB 或 k≤kPA,
即 k≥
=
,或 k≤
=-4,
∴k≥
,或k≤-4,
故选:C.
 解:如图所示:由题意得,所求直线l的斜率k满足 k≥kPB 或 k≤kPA,
解:如图所示:由题意得,所求直线l的斜率k满足 k≥kPB 或 k≤kPA,即 k≥
| 1+2 |
| 1+3 |
| 3 |
| 4 |
| 1+3 |
| 1-2 |
∴k≥
| 3 |
| 4 |
故选:C.
点评:本题考查直线的斜率公式的应用,体现了数形结合的数学思想.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
已知向量
=(-2,3),
=(3,1),则向量2
-
为( )
| m |
| n |
| m |
| n |
| A、(-1,5) |
| B、(-1,7) |
| C、(-7,5) |
| D、(-7,7) |
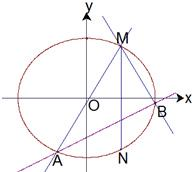 (2010•台州二模)已知两点M(2,3),N(2,-3)在椭圆
(2010•台州二模)已知两点M(2,3),N(2,-3)在椭圆