题目内容
对实数a和b,定义运算“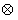 ”:
”: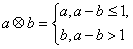 。设函数f(x)=(x2-2)
。设函数f(x)=(x2-2)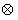 (x-1),x∈R。若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
(x-1),x∈R。若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
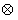 ”:
”: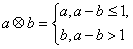 。设函数f(x)=(x2-2)
。设函数f(x)=(x2-2)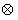 (x-1),x∈R。若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
(x-1),x∈R。若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是 [ ]
A.(-1,1]∪(2,+∞)
B.(-2,-1]∪(1,2]
C.(-∞,-2)∪(1,2]
D.[-2,-1]
B.(-2,-1]∪(1,2]
C.(-∞,-2)∪(1,2]
D.[-2,-1]
B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目