题目内容
自抛物线y2=2x上任意一点P向其准线l引垂线，垂足为Q，连接顶点O与P的直线和连接焦点F与Q的直线交于R点，求R点的轨迹方程．
解：设P（x1，y1）、R（x，y），则Q（-
，y1）、F（，0），
∴OP的方程为y=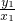
x，①
FQ的方程为y=-y1（x-）．②
由①②得x1=
，y1=
，
代入y2=2x，
可得y2=-2x2+x．
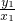分析：设P（x1，y1）、R（x，y），则Q（-，y1）、F（，0），由题意知OP的方程为y=x，FQ的方程为y=-y1（x-）．由此可求出R点的轨迹方程．
点评：本题考查轨迹方程的求法，解题时要认真审题，仔细解答．
，y1）、F（，0），∴OP的方程为y=
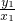x，①FQ的方程为y=-y1（x-
）．②由①②得x1=
，y1=，代入y2=2x，
可得y2=-2x2+x．
分析：设P（x1，y1）、R（x，y），则Q（-
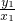，y1）、F（，0），由题意知OP的方程为y=x，FQ的方程为y=-y1（x-）．由此可求出R点的轨迹方程．点评：本题考查轨迹方程的求法，解题时要认真审题，仔细解答．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目