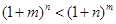题目内容
设函数![]() ,
,![]() .(Ⅰ)当
.(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;(Ⅱ)如果存在
处的切线方程;(Ⅱ)如果存在![]() ,使得
,使得![]() 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数![]() ;
;
(Ⅲ)如果对任意的![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【解析】:(Ⅰ)当![]() 时,
时,![]() ,
,![]() ,
,![]() …2分
…2分
所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(Ⅱ)![]() 使得
使得![]() 成立,等价于
成立,等价于![]() …4分
…4分
考虑![]()
|
| 0 |
|
|
| 2 |
|
| 0 | - | 0 | + | |
|
|
| 递减 | 极(最)小值 | 递增 | 1 |
由上表可知,![]() …………………………7分
…………………………7分
![]() 所以满足条件的最大整数
所以满足条件的最大整数![]() …………8分
…………8分
(Ⅲ)对任意的![]() ,都有
,都有![]() ,等价于:在区间
,等价于:在区间![]() 上,函数
上,函数![]() 的最小值不小于
的最小值不小于![]() 的最大值……9分有(2)知,在区间
的最大值……9分有(2)知,在区间![]() 上,
上,![]() 的最大值为
的最大值为![]()
![]() ,等价于
,等价于![]() 恒成立…………………………10分
恒成立…………………………10分
记![]() …………………11分
…………………11分
记![]() 由于
由于![]() ,
,
![]() ,所以
,所以![]() 在
在![]() 上递减,
上递减,
当![]() 时,
时,![]() ,
,![]() 时,
时,![]()
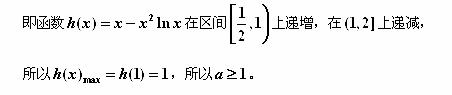

练习册系列答案
相关题目
 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意实数
,且对任意实数 ,都有
,都有 成立,数列
成立,数列 满足
满足 且
且
 的值;
的值; 对一切
对一切 均成立,求
均成立,求 的最大值.
的最大值. (
( ).
). 时,求
时,求 的极值;
的极值; 时,求
时,求 ,其中
,其中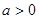 .
. 时,求不等式
时,求不等式 的解集;
的解集; 的解集为
的解集为 ,求
,求 的值.
的值.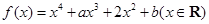 ,其中
,其中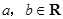 .
.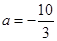 时,讨论函数
时,讨论函数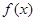 的单调性;
的单调性; 处有极值,求
处有极值,求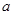 的取值范围;
的取值范围;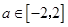 ,不等式
,不等式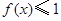 在
在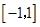 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.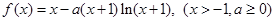
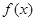 的单调区间;
的单调区间; 时,若方程
时,若方程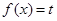 在
在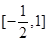 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;