题目内容
投到某杂志的稿件,先由两位初审专家进行评审.若能通过两位初审专家的评审,则予以录用;若两位初审专家都未予通过,则不予录用;若恰能通过一位初审专家的评审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录用.设稿件能通过各初审专家评审的概率均为0.5,复审的稿件能通过评审的概率为0.3.各专家独立评审.(Ⅰ)求投到该杂志的1篇稿件被录用的概率;
(Ⅱ)求投到该杂志的4篇稿件中,至少有2篇被录用的概率.
分析:(1)投到该杂志的1篇稿件被录用包括稿件能通过两位初审专家的评审或稿件恰能通过一位初审专家的评审又能通过复审专家的评审两种情况,这两种情况是互斥的,且每种情况中包含的事情有时相互独立的,列出算式.
(2)投到该杂志的4篇稿件中,至少有2篇被录用的对立事件是0篇被录用,1篇被录用两种结果,从对立事件来考虑比较简单.
(2)投到该杂志的4篇稿件中,至少有2篇被录用的对立事件是0篇被录用,1篇被录用两种结果,从对立事件来考虑比较简单.
解答:解:(Ⅰ)记A表示事件:稿件能通过两位初审专家的评审;
B表示事件:稿件恰能通过一位初审专家的评审;
C表示事件:稿件能通过复审专家的评审;
D表示事件:稿件被录用.
则D=A+B•C,
P(A)=0.5×0.5=0.25,
P(B)=2×0.5×0.5=0.5,
P(C)=0.3,
P(D)=P(A+B•C)
=P(A)+P(B•C)
=P(A)+P(B)P(C)
=0.25+0.5×0.3
=0.40.
(2)记4篇稿件有1篇或0篇被录用为事件E,
则P(E)=(1-0.4)4+C41×0.4×(1-0.4)3
=0.1296+0.3456
=0.4752,
∴P(
=1-0.4752=0.5248,
即投到该杂志的4篇稿件中,至少有2篇被录用的概率是0.5248.
B表示事件:稿件恰能通过一位初审专家的评审;
C表示事件:稿件能通过复审专家的评审;
D表示事件:稿件被录用.
则D=A+B•C,
P(A)=0.5×0.5=0.25,
P(B)=2×0.5×0.5=0.5,
P(C)=0.3,
P(D)=P(A+B•C)
=P(A)+P(B•C)
=P(A)+P(B)P(C)
=0.25+0.5×0.3
=0.40.
(2)记4篇稿件有1篇或0篇被录用为事件E,
则P(E)=(1-0.4)4+C41×0.4×(1-0.4)3
=0.1296+0.3456
=0.4752,
∴P(
. |
| E) |
即投到该杂志的4篇稿件中,至少有2篇被录用的概率是0.5248.
点评:本题关键是要理解题意,实际上能否理解题意是一种能力,培养学生的数学思想,提高发现问题、分析问题、解决问题的能力,增强学生数学思维情趣,形成学习数学知识的积极态度.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
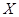 表示投到该杂志的4篇稿件中被录用的篇数,求
表示投到该杂志的4篇稿件中被录用的篇数,求 表示投到该杂志的4篇稿件中被录用的篇数,求
表示投到该杂志的4篇稿件中被录用的篇数,求