题目内容
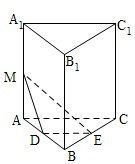 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=a,D,E分别为棱AB,BC的中点,M为棱AA1上的点,二面角M-DE-A为30°.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=a,D,E分别为棱AB,BC的中点,M为棱AA1上的点,二面角M-DE-A为30°.(I)证明:A1B1⊥C1D;
(II)求MA的长,并求点C到平面MDE的距离.
分析:(I)连接CD,根据三垂线定理可得AB⊥C1D,而A1B1平行AB,从而A1B1⊥C1D;
(II)过点A作CE的平行线,交ED的延长线于F,连接MF,根据定义可知∠MFA为二面角M-DE-A的平面角,在Rt△GAF中,∠GFA=30°,求出A到平面MDE的距离,再根据线面平行可知C到平面MDE的距离与A到平面MDE的距离相等.
(II)过点A作CE的平行线,交ED的延长线于F,连接MF,根据定义可知∠MFA为二面角M-DE-A的平面角,在Rt△GAF中,∠GFA=30°,求出A到平面MDE的距离,再根据线面平行可知C到平面MDE的距离与A到平面MDE的距离相等.
解答: 解:(I)证明:连接CD,
解:(I)证明:连接CD,
三棱柱ABC-A1B1C1是直三棱柱,∴CC1⊥平面ABC,∴CD为C1D在平面ABC内的射影.∵△ABC中,AC=BC,D为AB中点,∴AB⊥CD,∴AB⊥C1D∵A1B1∥AB,∴A1B1⊥C1D
(II)解:过点A作CE的平行线,
交ED的延长线于F,连接MF∵D,E分别为AB,BC的中点,∴DE∥AC
又∵AF∥CE,CE⊥AC∴AF⊥DE∵MA⊥平面ABC,∴AF为MF在平面ABC内的射影∴MF⊥DE∴∠MFA为二面角M-DE-A的平面角,∠MFA=30°
在Rt△MAF中,AF=
BC=
,∠MFA=30°,∴AM=
a
作AG⊥MF,垂足为G,∵MF⊥DE,AF⊥DE,∴DE⊥平面AMF,∵平面MDE⊥平面AMF,∴AG⊥平面MDE
在Rt△GAF中,∠GFA=30°,AF=
,∴AG=
,即A到平面MDE的距离为
∵CA∥DE,∴CA∥平面MDE,∴C到平面MDE的距离与A到平面MDE的距离相等,为
.
 解:(I)证明:连接CD,
解:(I)证明:连接CD,三棱柱ABC-A1B1C1是直三棱柱,∴CC1⊥平面ABC,∴CD为C1D在平面ABC内的射影.∵△ABC中,AC=BC,D为AB中点,∴AB⊥CD,∴AB⊥C1D∵A1B1∥AB,∴A1B1⊥C1D
(II)解:过点A作CE的平行线,
交ED的延长线于F,连接MF∵D,E分别为AB,BC的中点,∴DE∥AC
又∵AF∥CE,CE⊥AC∴AF⊥DE∵MA⊥平面ABC,∴AF为MF在平面ABC内的射影∴MF⊥DE∴∠MFA为二面角M-DE-A的平面角,∠MFA=30°
在Rt△MAF中,AF=
| 1 |
| 2 |
| a |
| 2 |
| ||
| 6 |
作AG⊥MF,垂足为G,∵MF⊥DE,AF⊥DE,∴DE⊥平面AMF,∵平面MDE⊥平面AMF,∴AG⊥平面MDE
在Rt△GAF中,∠GFA=30°,AF=
| a |
| 2 |
| a |
| 4 |
| a |
| 4 |
| a |
| 4 |
点评:本小题主要考查空间中的线面关系,解三角形等基础知识,考查空间想象能力与思维能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




