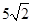题目内容
已知数列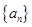 和
和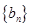 满足:
满足: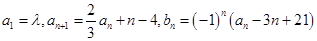 ,其中
,其中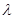 为实数,
为实数,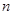 为正整数.
为正整数.
(1)对任意实数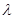 ,求证:
,求证: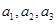 不成等比数列;
不成等比数列;
(2)试判断数列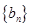 是否为等比数列,并证明你的结论.
是否为等比数列,并证明你的结论.
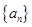 和
和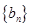 满足:
满足: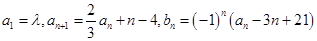 ,其中
,其中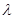 为实数,
为实数,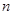 为正整数.
为正整数.(1)对任意实数
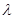 ,求证:
,求证: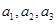 不成等比数列;
不成等比数列;(2)试判断数列
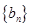 是否为等比数列,并证明你的结论.
是否为等比数列,并证明你的结论.(1)证明见解析;(2)当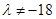 时,数列
时,数列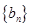 是等比数列.
是等比数列.
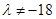 时,数列
时,数列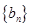 是等比数列.
是等比数列.试题分析:(1)证明否定性命题,可用反证法.如本题中可假设存在
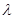 ,使
,使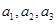 成等比数列,则可由
成等比数列,则可由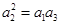 来求
来求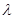 ,若求不出,说明假设错误,结论是不存在,
,若求不出,说明假设错误,结论是不存在,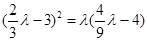 ,但这个式子化简后为
,但这个式子化简后为 ,不可能成立,即
,不可能成立,即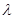 不存在;(2)要判定
不存在;(2)要判定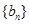 是等比数列,由题意可先求出
是等比数列,由题意可先求出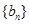 的递推关系,
的递推关系,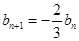 ,这时还不能说明
,这时还不能说明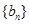 就是等比数列,还要求出
就是等比数列,还要求出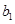 ,
,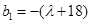 ,只有当
,只有当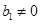 时,数列
时,数列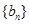 才是等比数列,因此当
才是等比数列,因此当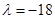 时,
时,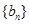 不是等比数列,当
不是等比数列,当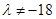 时,
时,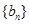 是等比数列.
是等比数列.(1)证明:假设存在一个实数
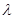 ,使
,使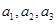 是等比数列,则有
是等比数列,则有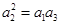 ,
,即
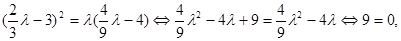 矛盾.
矛盾.所以
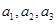 不成等比数列. 6分
不成等比数列. 6分(2)因为
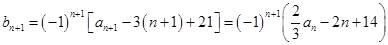
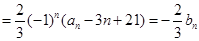 9分
9分又
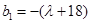 ,
,所以当
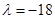 ,
,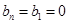 ,(
,(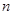 为正整数),此时
为正整数),此时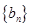 不是等比数列: 11分
不是等比数列: 11分当
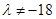 时,
时,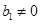 ,由上式可知
,由上式可知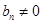 ,∴
,∴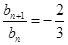 (
(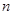 为正整数) ,
为正整数) ,故当
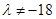 时,数列
时,数列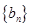 是以
是以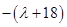 为首项,-
为首项,-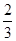 为公比的等比数列. 14分
为公比的等比数列. 14分
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
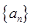 中,
中,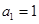 ,前
,前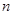 项的和是
项的和是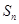 ,且
,且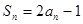 ,
,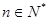 .
.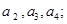
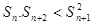 .
. 的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.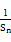 ≤
≤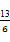 (n∈N*).
(n∈N*).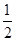 a3,a1成等差数列,则
a3,a1成等差数列,则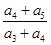 =( )
=( )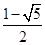
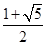
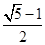
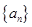 的前
的前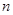 项和为
项和为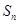 ,且对任意
,且对任意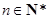 ,有
,有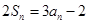 ,则
,则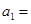 ;
;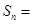 .
.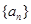 中
中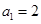 ,公比
,公比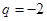 ,记
,记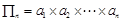 (即
(即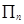 表示数列
表示数列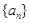 的前n项之积),
的前n项之积),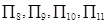 中值最大的是( )
中值最大的是( )

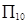

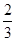 ,且对任意的正整数m,n,都有am+n=am·an,若数列{an}的前n项和为Sn,则Sn等于( )
,且对任意的正整数m,n,都有am+n=am·an,若数列{an}的前n项和为Sn,则Sn等于( )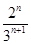
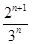
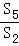 =( )
=( )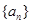 中,
中,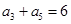 ,
,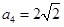 ,则
,则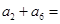 ( )
( )