题目内容
设函数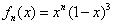 在
在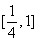 上的最大值为
上的最大值为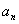 (
(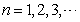 ).
).
(Ⅰ)求数列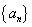 的通项公式;
的通项公式;
(Ⅱ)求证:对任何正整数n (n≥2),都有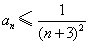 成立;
成立;
(III)设数列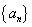 的前n项和为Sn,求证:对任意正整数n,都有
的前n项和为Sn,求证:对任意正整数n,都有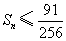 成立.
成立.
【解析】(Ⅰ)
 ,
,
当 时,由
时,由 知
知 或
或 ,
,
当 时,则
时,则 ,
, 时,
时, ,
,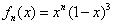 在
在 上单调递减,
上单调递减,
所以
当 时,
时, ,
, 时,
时, ,
, 时,
时, ,
,
∴ 在
在 处取得最大值,即
处取得最大值,即

 当
当 时,由(II)知
时,由(II)知


 .
.
所以,对任意正整数 ,都有
,都有 成立.
成立.

练习册系列答案
相关题目
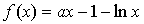
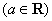 .
.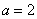 时,求函数
时,求函数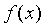 的单调区间;
的单调区间;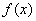 在
在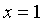 处取得极值,对
处取得极值,对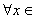
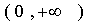 ,
, 恒成立,求实数
恒成立,求实数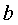 的取值范围;
的取值范围;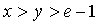 时,求证:
时,求证: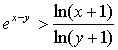 .
. 中,若
中,若 ,则有
,则有
 成立.类比上述性质,在等比数列
成立.类比上述性质,在等比数列 中,若
中,若 ,则有 .
,则有 . 在区间(0,1)内任取两个实数p,q,且p≠q,不等式
在区间(0,1)内任取两个实数p,q,且p≠q,不等式 恒成立,则实数
恒成立,则实数 的取值范围为
的取值范围为 B.
B. C.
C. D.
D.
 .
. ,求f(B)的取值范围.
,求f(B)的取值范围. ,且
,且 ,则
,则 的取值范围是
的取值范围是
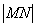 的最大值为
的最大值为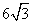 (B)
(B) 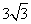 (C)
(C) 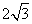 (D)3
(D)3 ,运算原理如图所示,则式子
,运算原理如图所示,则式子 的值为
的值为  是正
是正 三边的中点,由
三边的中点,由 六点中的两点构成的向量中与
六点中的两点构成的向量中与 共线(
共线( .
.
 .
.
 .
.
 .
.
