题目内容
(本小题满分13分)有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示:

(1)求频率分布直方图中 的值;
的值;
(2)分别求出成绩落在 中的学生人数;
中的学生人数;
(3)从成绩在 的学生中任选2人,求所选学生的成绩都落在
的学生中任选2人,求所选学生的成绩都落在 中的概率.
中的概率.
(1) ; (2)成绩落在
; (2)成绩落在 中的学生人数为
中的学生人数为 ,成绩落在
,成绩落在 中的学生人数
中的学生人数
成绩落在 中的学生人数
中的学生人数 ;(3)
;(3) .
.
【解析】
试题分析:
(1)种用频率分布直方图的意义,所有小长方形的面积和为1列方程即可;
(2)利用(1)的结果分别求出数据每个区间内的频率,从而求出成绩落在 中的学生人数;
中的学生人数;
(3)由(2)知,成绩落在的学生共有6人,其中成绩落在 中的学生人数为
中的学生人数为 ,记落在
,记落在 中的学生为
中的学生为 ,落在
,落在 中的学生为
中的学生为 ,利用古典概型的概率计算公式可求所选学生的成绩都落在
,利用古典概型的概率计算公式可求所选学生的成绩都落在 中的概率.
中的概率.
试题解析:【解析】
(1)由题意 ,
, . 3分
. 3分
(2)成绩落在 中的学生人数为
中的学生人数为 ,
,
成绩落在 中的学生人数
中的学生人数
成绩落在 中的学生人数
中的学生人数 . 6分
. 6分
(3)设落在 中的学生为
中的学生为 ,落在
,落在 中的学生为
中的学生为 ,
,
则 ,基本事件个数为
,基本事件个数为 ,
,
设A=“此2人的成绩都在 ”,则事件A包含的基本事件数
”,则事件A包含的基本事件数 ,
,
所以事件A发生概率 . 13分
. 13分
考点:1、频率分布直方图;2、古典概型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的不等式组
的不等式组 表示一个三角形区域,则实数
表示一个三角形区域,则实数 的取值范围是______.
的取值范围是______. 有零点”是“函数
有零点”是“函数 在(0,+∞)上为减函数”的( )
在(0,+∞)上为减函数”的( ) 的图像可能是( ) .
的图像可能是( ) .



 则
则 ( ).
( ). B.
B.
 D.
D.
 ,
, 满足约束条件
满足约束条件 则
则 的最大值是 .
的最大值是 .
 B.
B.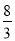 C.
C.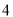 D.
D.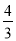
 中,角
中,角 对应的边分别为
对应的边分别为 .若
.若 则“
则“ ”是“
”是“ ”的
”的 ,若函数
,若函数 ,则
,则 的解集为( )
的解集为( ) B.
B. C.
C. D.
D.