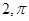题目内容
函数
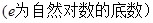 的零点个数为( )
的零点个数为( )
A. | B. | C. | D. |
B
解析试题分析:函数 在
在 上是增函数,
上是增函数,
∵
可得函数 在
在 上有唯一零点,
上有唯一零点,
故选B.
考点:函数零点存在定理,函数的单调性.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知函数 的三个实数根分别为
的三个实数根分别为 ,则
,则 的范围是( )
的范围是( )
A. | B. | C. | D. |
若函数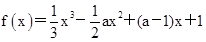 在区间(1,4)内为减函数,在区间(6,+∞)内为增函数,则实数a的取值范围是 ( )
在区间(1,4)内为减函数,在区间(6,+∞)内为增函数,则实数a的取值范围是 ( )
| A.a≤2 | B.5≤a≤7 | C.4≤a≤6 | D.a≤5或a≥7 |
若函数 ,则函数
,则函数 ( )
( )
A.是奇函数,在 是增函数 是增函数 | B.是偶函数,在 是减函数 是减函数 |
C.是偶函数,在 是增函数 是增函数 | D.是奇函数,在 是减函数 是减函数 |
若直线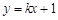 与曲线
与曲线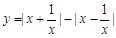 有四个公共点,则
有四个公共点,则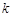 的取值集合是( )
的取值集合是( )
A.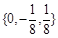 | B.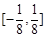 | C.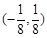 | D.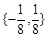 |
下列函数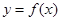 中满足“对任意
中满足“对任意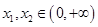 ,当
,当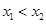 时,都有
时,都有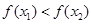 ”的是( )
”的是( )
A.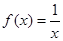 | B.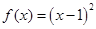 | C.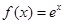 | D. |
函数 的定义域是 ( )
的定义域是 ( )
A.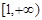 | B.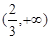 | C.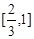 | D.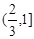 |
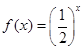 ,则函数
,则函数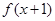 的反函数的图象可能是( )
的反函数的图象可能是( )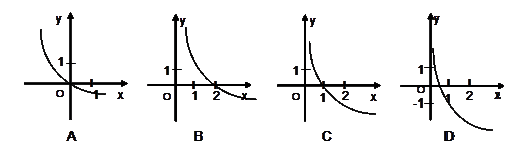
 ,
,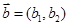 ,定义一运算:
,定义一运算: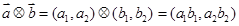 ,已知
,已知 ,
, .点Q在
.点Q在 的图像上运动,且满足
的图像上运动,且满足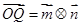 (其中O为坐标原点),则
(其中O为坐标原点),则