题目内容
已知定义在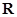 上的奇函数
上的奇函数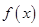 满足
满足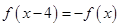 ,且
,且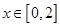 时,
时,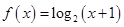 ,有下列结四个论:
,有下列结四个论:
①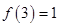 ;
;
②函数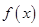 在
在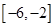 上是增函数;
上是增函数;
③函数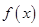 关于直线
关于直线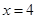 对称;
对称;
④若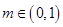 ,则关于
,则关于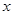 的方程
的方程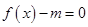 在
在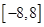 上所有根之和为-8.
上所有根之和为-8.
其中正确的是________(写出所有正确命题的序号)
①④
解析试题分析:取 得,
得, ,所以
,所以 ,①正确;定义在R上的奇函数
,①正确;定义在R上的奇函数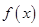 满足
满足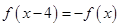 ,则
,则 ,
, ,∴函数
,∴函数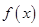 关于直线
关于直线 对称,故③不正确;奇函数
对称,故③不正确;奇函数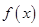 ,
,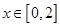 时,
时,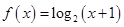 ,
, 时,函数为单调增函数,∵函数
时,函数为单调增函数,∵函数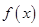 关于直线
关于直线 对称,∴函数
对称,∴函数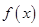 在
在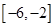 上是减函数,故②不正确;若
上是减函数,故②不正确;若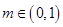 ,则关于
,则关于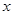 的方程
的方程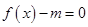 在
在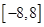 上有
上有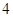 个根,其中两根的和为
个根,其中两根的和为 ,另两根的和为
,另两根的和为 ,所以所有根之和为
,所以所有根之和为 .故④正确,答案①④.
.故④正确,答案①④.
考点:奇函数的性质、函数的对称性、函数的增减性、函数与方程.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 上的函数
上的函数 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若 ,且当
,且当 时,
时, ,则
,则 的值为_________.
的值为_________.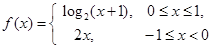 的值域是______________.
的值域是______________. 解集为空集,则满足条件的实数a的值为 .
解集为空集,则满足条件的实数a的值为 .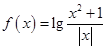
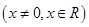 有如下命题:
有如下命题: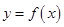 图像关于
图像关于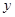 轴对称.
轴对称. 时,
时,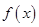 是增函数,
是增函数,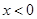 时,
时,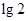 .
.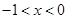 或
或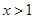 时.
时.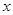 的方程
的方程 有实根,则实数
有实根,则实数 的取值范围是 .
的取值范围是 . ,若
,若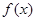 是奇函数,则
是奇函数,则 .
.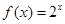 且
且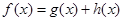 ,其中
,其中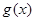 为奇函数,
为奇函数, 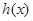 为偶函数,若不等式
为偶函数,若不等式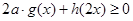 对任意
对任意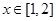 恒成立,则实数
恒成立,则实数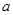 的取值范围是 .
的取值范围是 .