题目内容
在等腰直角三角形ABC中,C=90°,直角边BC在直线2x+3y-6=0上,顶点A的坐标是(5,4),求边AB 和AC所在的直线方程.
解:AC的斜率k1= ,∴AC所在的直线方程为 y-4=
,∴AC所在的直线方程为 y-4= (x-5),即 3x-2y-7=0.
(x-5),即 3x-2y-7=0.
设直线AB的方向向量为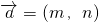 ,又直线AC的方向向量
,又直线AC的方向向量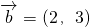 ,且<
,且< ,
, >=45°,
>=45°,
所以, ,∴2(2m+3n)2=13(m2+n2),
,∴2(2m+3n)2=13(m2+n2),
∴ ,
,
故直线AB的方向向量为 ,
,
即 直线AB的斜率 .∴AB所在的直线方程为 y-4=-5(x-5),或 y-4=
.∴AB所在的直线方程为 y-4=-5(x-5),或 y-4= (x-5),
(x-5),
即:5x+y-29=0或x-5y+15=0.
分析:由垂直关系求得AC斜率,点斜式求AC所在的直线方程.设出直线AB的方向向量,由AB和AC夹角等于45°,
求出AB的方向向量,即得它的斜率,点斜式求出 AB所在的直线方程.
点评:本题考查用点斜式求直线方程的方法,直线的方向向量及两个向量的夹角公式得应用,求直线AB的斜率是解题的难点和关键.
 ,∴AC所在的直线方程为 y-4=
,∴AC所在的直线方程为 y-4= (x-5),即 3x-2y-7=0.
(x-5),即 3x-2y-7=0.设直线AB的方向向量为
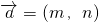 ,又直线AC的方向向量
,又直线AC的方向向量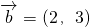 ,且<
,且< ,
, >=45°,
>=45°,所以,
 ,∴2(2m+3n)2=13(m2+n2),
,∴2(2m+3n)2=13(m2+n2),∴
 ,
,故直线AB的方向向量为
 ,
,即 直线AB的斜率
 .∴AB所在的直线方程为 y-4=-5(x-5),或 y-4=
.∴AB所在的直线方程为 y-4=-5(x-5),或 y-4= (x-5),
(x-5),即:5x+y-29=0或x-5y+15=0.
分析:由垂直关系求得AC斜率,点斜式求AC所在的直线方程.设出直线AB的方向向量,由AB和AC夹角等于45°,
求出AB的方向向量,即得它的斜率,点斜式求出 AB所在的直线方程.
点评:本题考查用点斜式求直线方程的方法,直线的方向向量及两个向量的夹角公式得应用,求直线AB的斜率是解题的难点和关键.

练习册系列答案
相关题目
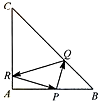 在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到点P(如图).若光线QR经过△ABC的重心(三角形三条中线的交点),则AP=
在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到点P(如图).若光线QR经过△ABC的重心(三角形三条中线的交点),则AP=