题目内容
关于x的方程（x2-1）2-|x2-1|+k=0有5个不同的实根，则实数k= ．
【答案】分析：讨论x2-1的正负，画出高次函数的图象，观察即可得出答案．
解答：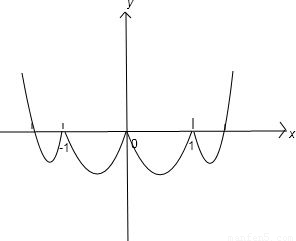
解：当x2-1≥0时原方程为
（x2-1）（x2-2）=-k
（x-1）（x+1）（x+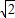
）（x-
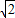）=-k
当x＜0时原方程为
（x2-1）x2=-k
（x+1）（x-1）x2=-k
两种情况联立图象为
由此可知只有当k=0时，方程才可能有五个不同实根．
故答案为0．
点评：本题考查了高次方程的解，技巧有把高次方程因式分解，把所有根在数轴上从小到大依次排列，用平滑曲线从右上方开始顺次穿过所有根，值得注意的是如果根所在的因式为偶次曲线穿而不过，像图中的-1，0，1处．在x轴上下方的线分别代表y的值的正负．
解答：
解：当x2-1≥0时原方程为（x2-1）（x2-2）=-k
（x-1）（x+1）（x+
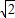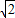）（x-）=-k当x＜0时原方程为
（x2-1）x2=-k
（x+1）（x-1）x2=-k
两种情况联立图象为
由此可知只有当k=0时，方程才可能有五个不同实根．
故答案为0．
点评：本题考查了高次方程的解，技巧有把高次方程因式分解，把所有根在数轴上从小到大依次排列，用平滑曲线从右上方开始顺次穿过所有根，值得注意的是如果根所在的因式为偶次曲线穿而不过，像图中的-1，0，1处．在x轴上下方的线分别代表y的值的正负．
练习册系列答案
相关题目