题目内容
直线y=2x是△ABC中∠C的平分线所在的直线,若A、B坐标分别为A(-4,2)、B(3,1),求点C的坐标,并判断△ABC的形状.
解：由题意,点A关于直线y=2x的对称点A′在BC所在直线上,设A′点坐标为(x1,y1),则x1、y1满足
=-
,即x1=-2y1. ①
=2·
,即2x1-y1-10=0. ②
解①②两式组成的方程组,得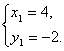
∴BC所在直线方程为
=
,
即3x+y-10=0.解方程组
得
∴所求C点坐标为(2,4).
由题意|AB|2=50,|AC|2=40,|BC|2=10,∴△ABC为直角三角形.
练习册系列答案
相关题目