题目内容
已知向量 .
.(1)当
 的值;
的值;(2)求
 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
【答案】分析:(1)利用向量共线的条件,可得tanx=1,再将2cos2x-sin2x为关于tanx的函数,即可求得结论;
(2)利用向量的数量积运算,并化简函数 ,即可求得函数的最小正周期与单调递增区间.
,即可求得函数的最小正周期与单调递增区间.
解答:解:(1)∵ ,
, .
.
∴sinx-cosx=0即tanx=1
∴2cos2x-sin2x= =
= =0
=0
(2) =sinxcosx+1=
=sinxcosx+1= sin2x+1
sin2x+1
∴ 的最小正周期为T=
的最小正周期为T= =π,
=π,
- +2kπ≤2x≤
+2kπ≤2x≤ +2kπ
+2kπ
解得- +kπ≤x≤
+kπ≤x≤ +kπ,k∈Z
+kπ,k∈Z
∴单调递增区间[- +kπ,
+kπ, +kπ],k∈Z
+kπ],k∈Z
点评:本题主要考查了向量知识的运用,考查三角函数的化简,考查三角函数的性质,同时考查了运算求解的能力,属于中档题.
(2)利用向量的数量积运算,并化简函数
 ,即可求得函数的最小正周期与单调递增区间.
,即可求得函数的最小正周期与单调递增区间.解答:解:(1)∵
 ,
, .
.∴sinx-cosx=0即tanx=1
∴2cos2x-sin2x=
 =
= =0
=0(2)
 =sinxcosx+1=
=sinxcosx+1= sin2x+1
sin2x+1∴
 的最小正周期为T=
的最小正周期为T= =π,
=π,-
 +2kπ≤2x≤
+2kπ≤2x≤ +2kπ
+2kπ解得-
 +kπ≤x≤
+kπ≤x≤ +kπ,k∈Z
+kπ,k∈Z∴单调递增区间[-
 +kπ,
+kπ, +kπ],k∈Z
+kπ],k∈Z点评:本题主要考查了向量知识的运用,考查三角函数的化简,考查三角函数的性质,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目
 .
. 的值.
的值.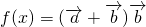 的最小正周期和单调递增区间.
的最小正周期和单调递增区间. .
. 的值.
的值. 的最小正周期和单调递增区间.
的最小正周期和单调递增区间. .
. 的值.
的值. 的最小正周期和单调递增区间.
的最小正周期和单调递增区间. .
. 的值.
的值. 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.