Question

【题目】设关于的方程有两个实根，函数.

（1）求的值；

（2）判断在区间的单调性，并加以证明；

（3）若均为正实数，证明：

Answer 1

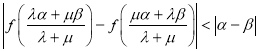
【答案】（1）＋；（2）单调递增；（3）见解析.

【解析】

试题（1）因为是方程的的两个实根，利用韦达定理即可得到的解析式，求出进而即可求出的值；（2）利用导数及二次函数的图像来讨论导数的正负，即可判断函数的单调性；（3）首先求出的取值范围，然后根据函数的单调性判断出函数值的取值范围，把两个函数值相减即可得到要证的结论.

试题解析：（1）∵是方程的两个根， ∴，， 1分

∴，又，∴， 3分

即，同理可得

∴＋ 4分

（2）∵， 6分

将代入整理的 7分

又，∴在区间的单调递增; 8分

（3）∵，

∴ 10分

由（2）可知，同理

12分

由（1）可知，，，

∴

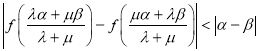∴ 14分