题目内容
(本小题满分10分)河上有一抛物线型拱桥,当水面距拱顶5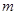 时,水面宽为8
时,水面宽为8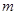 ,一小船宽4
,一小船宽4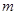 ,高2
,高2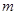 ,载货后船露出水面上的部分高
,载货后船露出水面上的部分高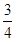
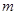 ,问水面上涨到与抛物线拱顶相距多少米时,小船恰好能通行。
,问水面上涨到与抛物线拱顶相距多少米时,小船恰好能通行。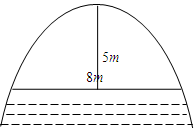
2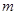 。
。
解析试题分析:建立直角坐标系,设抛物线型拱桥方程为 ,过A(-4,-5),B(4,-5),
,过A(-4,-5),B(4,-5), ,
, ,由于小船宽4
,由于小船宽4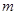 ,当
,当 时,
时, ,即当船顶距抛物线拱顶为
,即当船顶距抛物线拱顶为 时,小船恰好能通过。又载货后,船露出水面上的部分高
时,小船恰好能通过。又载货后,船露出水面上的部分高 。当水面距抛物线拱顶距离
。当水面距抛物线拱顶距离 时,小船恰好能通行。
时,小船恰好能通行。
答:当水面上涨到与抛物线拱顶相距2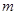 时,小船恰好能通行。
时,小船恰好能通行。
考点:抛物线的实际应用。
点评:本题主要考查了抛物线的实际应用,是中档题.解题时要认真审题,恰当地建立坐标系,合理地进行等价转化.

练习册系列答案
相关题目
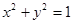 过椭圆
过椭圆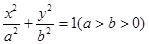 的两焦点,与椭圆有且仅有两个
的两焦点,与椭圆有且仅有两个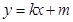 与圆
与圆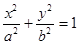 相交于
相交于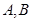 两点记
两点记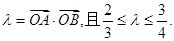
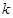 的取值范围;
的取值范围;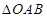 的面积S的取值范围.
的面积S的取值范围. 是椭圆
是椭圆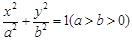 上一点,
上一点,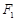 ,
,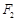 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足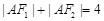
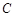 、
、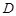 是椭圆上任两点,且直线
是椭圆上任两点,且直线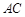 、
、 的斜率分别为
的斜率分别为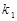 、
、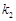 ,若存在常数
,若存在常数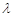 使
使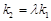 ,求直线
,求直线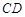 的斜率.
的斜率. 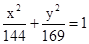 有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.
有共同焦点,且过点(0,2)的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率以及渐近线方程.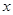 轴上,左右焦点分别为
轴上,左右焦点分别为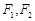 ,且
,且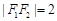 ,
,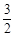 )在椭圆C上.
)在椭圆C上.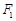 的直线
的直线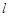 与椭圆
与椭圆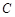 相交于
相交于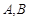 两点,且
两点,且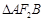 的面积为
的面积为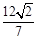 ,求直线
,求直线 轴的负半轴上,过点
轴的负半轴上,过点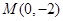 作直线
作直线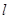 与抛物线交于A,B两点,且满足
与抛物线交于A,B两点,且满足 ,
,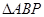 面积的的最大值.
面积的的最大值.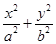 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆点,椭圆的短半轴为半径的圆与直线x-y+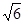 =0相切。
=0相切。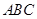 内有一动点
内有一动点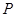 ,已知
,已知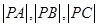 ,且满足
,且满足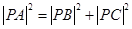 ,求
,求